المنطق الأرسطي Aristotelian Logic
قوام المنطق هو الحجج، وقوام الحجة هو القضايا. في الحلقات السابقة ناقشنا بقدر من التفصيل أساليب اللغة المستخدمة عند صياغة القضايا، لكن اللغة أحد أدوات صناعة الحجة، الاداة الاخرى هي التركيب أو العلاقات بين قضايا الحجة. الحجج الاستنتاجية deductive arguments هي الجدليات التي ندعي أن قضايا المقدمة بها تبرهن بما لا يدع مجال للشك على النتيجة. اى ان البرهان مطلق حول حقيقة نتيجة الحجة. إن صح ادعاء المقدمة اى ان كانت قضايا المقدمة حقيقية، إذن لابد من حقيقة النتيجة، وفي تلك الحالة يطلق على الحجة الاستنتاجية صالحة Valid. الحجة الاستنتاجية قد تكون في حالة واحدة ممكنة فقط من حالتين إما صالحة أو غير صالحة. وبالتالي الحجة الاستنتاجية الصالحة  لابد أن تبرهن مقدماتها على نتيجتها (أرجع لحلقة أسس علم المنطق). الاستنتاج Deduction يسعى لتفسير العلاقات بين المقدمات والنتيجة في الحجج الاستنتاجية. من خلال وضع طرق وآليات لتقييم صلاحية الحجة. الفلاسفة وعلماء المنطق وضعوا نظريتين أساسيتين للاستنتاج داخل علم المنطق. الأولى هي منظومة المنطق الكلاسيكي classical logic او يطلق عليها البعض المنطق الأرسطي Aristotelian logic نسبة لمؤسس المنظومة الفيلسوف الإغريقي أرسطو. والثانية هي منظومة المنطق الحديث modern logic أو المنطق الرمزي symbolic logic التى تطورت خلال القرن التاسع عشر والعشرين. في الحقيقة أرسطو Aristotle كان أحد القمم العقلية الشاهقة في العالم القديم، بعد دراسته في أكاديمية أفلاطون، أصبح معلم للأسكندر الأكبر، وبعدها قام بتأسيس مدرسته الخاصة الليسيوم Lyceum التي من خلالها شارك أرسطو تقريبا في كافة المجالات العقلية والبحثية المعروفة وقتها، وساهم تقريبا في كافة مناحي المعرفة البشرية. ومساهمته الكبرى حول العقلانية البشرية وجدت بعد موته وعرفت الارغانون Organon أى الالة، آلة المعرفة الانسانية. لكن مصطلح المنطق Logic لم يجد طريقة الى اللغات البشرية حتى القرن الثاني قبل الميلاد، لكن معناه والقضية التى ناقشها عرفت قبل اسمة بقرون عديدة على يد أرسطو في الارغونان. والمنطق الأرسطي كان ومازال القاعدة المتينة لعملية التفكير والتحليل العقلاني منذ الالاف السنين. خلال تلك السنين تم إعادة صياغة الكثير من مبادئه وتعريف العديد من قواعد، وتحسين وتطوير أدواته، لكن بقت هذه المنظومة الكلاسيكية للعقلانية قوة هائلة ناعمة لمن أمتلكها. الأورغانون شمل ست كتب رئيسية
لابد أن تبرهن مقدماتها على نتيجتها (أرجع لحلقة أسس علم المنطق). الاستنتاج Deduction يسعى لتفسير العلاقات بين المقدمات والنتيجة في الحجج الاستنتاجية. من خلال وضع طرق وآليات لتقييم صلاحية الحجة. الفلاسفة وعلماء المنطق وضعوا نظريتين أساسيتين للاستنتاج داخل علم المنطق. الأولى هي منظومة المنطق الكلاسيكي classical logic او يطلق عليها البعض المنطق الأرسطي Aristotelian logic نسبة لمؤسس المنظومة الفيلسوف الإغريقي أرسطو. والثانية هي منظومة المنطق الحديث modern logic أو المنطق الرمزي symbolic logic التى تطورت خلال القرن التاسع عشر والعشرين. في الحقيقة أرسطو Aristotle كان أحد القمم العقلية الشاهقة في العالم القديم، بعد دراسته في أكاديمية أفلاطون، أصبح معلم للأسكندر الأكبر، وبعدها قام بتأسيس مدرسته الخاصة الليسيوم Lyceum التي من خلالها شارك أرسطو تقريبا في كافة المجالات العقلية والبحثية المعروفة وقتها، وساهم تقريبا في كافة مناحي المعرفة البشرية. ومساهمته الكبرى حول العقلانية البشرية وجدت بعد موته وعرفت الارغانون Organon أى الالة، آلة المعرفة الانسانية. لكن مصطلح المنطق Logic لم يجد طريقة الى اللغات البشرية حتى القرن الثاني قبل الميلاد، لكن معناه والقضية التى ناقشها عرفت قبل اسمة بقرون عديدة على يد أرسطو في الارغونان. والمنطق الأرسطي كان ومازال القاعدة المتينة لعملية التفكير والتحليل العقلاني منذ الالاف السنين. خلال تلك السنين تم إعادة صياغة الكثير من مبادئه وتعريف العديد من قواعد، وتحسين وتطوير أدواته، لكن بقت هذه المنظومة الكلاسيكية للعقلانية قوة هائلة ناعمة لمن أمتلكها. الأورغانون شمل ست كتب رئيسية
(1) كتاب المقولات The Categories وهو الكتاب الذي عالج فيه أرسطو التصورات الأساسية
(2) كتاب التأويل On Interpretation وأهتم فيه أرسطو بتحليل القضايا والاحكام
(3) كتاب التحليلات الأولى The First Analytics وهو الموضع الأول في الأورغانون الذى عرض فيه أرسطو نظرية القياس
(4) كتاب التحليلات الثانية The Second Analytics المكون من جزئين وعالج فيها أرسطو بقدر كبير من التفصيل نظرية البرهان
(5) كتاب الجدل أو الطوبيقا Topics المتكون من ثمان أجزاء رئيسية لخص فيها أرسطو كل ما يتعلق بالجدل، البرهان الاحتمالي أو نظرية الاحتمال.
(6) وأخيرا كتاب دحض المغالطات أو السفسطيات On sophistical refutations وعالج فيه بتفصيل كبيرة تصنيفه للمغالطات المنطقية وطرق دحضها والذى تعرضنا له بقدر من التفصيل في الحلقتين السابقتين.
وفي الواقع أرسطو في تصنيفية للعلوم وضع المنطق خارج هذا التصنيف الامر الذى كان ومازال موضع حيرة وبحث الدارسين، قد يكون هذا لان أرسطو أراد تمييز المنطق عن بقية العلوم من حيث اتصالها المباشر بالواقع في حين أن المنطق يتمثل في تحقيق غاية منهجية كلية لا تتصل بشكل مباشر بالواقع الخارجي كما هو الحال في غاية العلوم الطبيعية. وقد يكون لان قضايا العلم عند أرسطو كما كانت ومازالت عند العلماء غير قابلة للبرهان القطعي دائما، في حين ان المنطق ليس كذلك. أيا كان السبب وراء عدم تصنيف أرسطو للمنطق داخل تصنيفية للعلوم الطبيعية ( الأمر المتخصص والخارج عن إطار بحثنا الحالي)، أرسطو فطن لان المنطق ضروري لكل العلوم الطبيعية، أو هو نسق القواعد التى من خلالها يمكن الاستنباط، وبالتالي تمكن العلم كآلة أستنباطنية في الواقع الخارجي. وبالتالي المنطق عند أرسطو ليس علما كسائر العلوم، وإنما هو علم كل العلوم وبالتالي لا يمكن تصنيفه أو إدراجه داخل تصنيف العلوم، لأنها قائمة عليه وضعية محدودة بالزمان والمكان، أما المنطق كلي غير محدود لا بالزمان أو المكان.
حيرة وبحث الدارسين، قد يكون هذا لان أرسطو أراد تمييز المنطق عن بقية العلوم من حيث اتصالها المباشر بالواقع في حين أن المنطق يتمثل في تحقيق غاية منهجية كلية لا تتصل بشكل مباشر بالواقع الخارجي كما هو الحال في غاية العلوم الطبيعية. وقد يكون لان قضايا العلم عند أرسطو كما كانت ومازالت عند العلماء غير قابلة للبرهان القطعي دائما، في حين ان المنطق ليس كذلك. أيا كان السبب وراء عدم تصنيف أرسطو للمنطق داخل تصنيفية للعلوم الطبيعية ( الأمر المتخصص والخارج عن إطار بحثنا الحالي)، أرسطو فطن لان المنطق ضروري لكل العلوم الطبيعية، أو هو نسق القواعد التى من خلالها يمكن الاستنباط، وبالتالي تمكن العلم كآلة أستنباطنية في الواقع الخارجي. وبالتالي المنطق عند أرسطو ليس علما كسائر العلوم، وإنما هو علم كل العلوم وبالتالي لا يمكن تصنيفه أو إدراجه داخل تصنيف العلوم، لأنها قائمة عليه وضعية محدودة بالزمان والمكان، أما المنطق كلي غير محدود لا بالزمان أو المكان.

محاور
المنطق الأرسطي، الفئات و القضايا الحملية، أنواع القضايا الحملية، مخططات فيين، تشريح القضايا الحملية، مربع ارسطو، صور أخرى للاستدلال المباشر، الاستدلال بنقض المحمول (التغيير)، الاستدلال بالتعارض، المضمون الوجودي، مربع التقابل الحديث، المغالطة الوجودية، جوهر منطق أرسطو
الفئات و القضايا الحملية Classes and Categorical Propositions
المنطق الكلاسيكي يتعامل في الأساس مع الحجج حول فئات من الأشياء وعلاقتها ببعضها البعض. الفئة Class هي مجموعة من الكائنات او الاشياء التى تشترك في خواص معينة (أرجع لحلقة المعنى والمنطق). اى كائن يمتلك كفاءة منطقية عقلية يستطيع أن يصنف العلاقات بين الفئات بديهيا في ثلاثة صور (1) كل أعضاء فئة ما جزء من فئة أخرى. مثلا كل الرجال بشر، اى ان كل اعضاء فئة الرجال بالكامل جزء من فئة أخرى وهى البشر (2) بعض، لكن ليس كل، أعضاء فئة معينة قد تكون جزء من فئة أخرى. مثلا كل المهندسين من الرجال. أى أن بعض أعضاء فئة المهندسين قد يكونوا جزء من فئة اخرى وهي الرجال، لأن هناك مهندسين من النساء مثلا. (3) فئتين لا توجد بينهما أى أعضاء مشتركة على الاطلاق. مثلا فئة كل النساء تستبعد exclude فئة الرجال. اى ان لا يمكن أن يوجد عضو من فئة النساء ينتمي أيضا لفئة الرجال…. العقل المنطقي قادر على تطبيق تلك العلاقات على اى مجموعة من الفئات او التصنيفات. في الحجج الاستنتاجية نقدم قضايا حول العلاقات بين فئة وأخرى. علماء المنطق يطلقوا على هذا النوع من القضايا، القضايا الحملية categorical propositions و البعض يطلق عليها المطلقة لان برهان حقيقتها مطلق لا مجال للشك فيه، و البعض الاخر يطلق عليها التصنيفية لأن الحقيقة فيها قائمة على العلاقات بين التصنيفات او الفئات، وأخيرا بعض المناطقة يطلقوا عليها القضية ذات صور الموضوع-المحمول Subject-Predict Proposition كما سنرى بعد قليل. لكن جرت العادة في الكتابات العربية على الاشارة لهذا النوع بالقضايا الحملية نسبة إلى معامل الحمل. في علم المنطق الكلاسيكي او الأرسطي القضايا الحملية احد العناصر الاساسية لبناء الحجج الاستنتاجية. تأمل هذة الحجة (1) لايوجد شخص من أصل عربي بوذي (2) كل المصريين من أصل عربي (3) إذن لا يوجد مصريين بوذيين. هذه الحجة تحتوى على ثلاث قضايا حملية. من الممكن ان نشكك أو ننفي حقيقة ايا منهم، لكن العلاقات بين الفئات كما تم التعبير عنها في تلك القضايا تؤدى الى حجة صالحة Valid اى ان صحت حقيقة المقدمات لابد من حقيقة النتيحة بما لا يدع مجال للشك. كل قضية من قضايا الحجة منفردة هي قضية حملية. اى ان كل قضية اما تأكد، او تنفي علاقة ما بين فئة س وفئة أخرى ص سواء بشكل كلي او جزئي. في هذا المثال العلاقات كانت بين فئات العرب، البوذين، والمصرين. وبالتالي كي نستطيع الوصول إلى منظومة للمنطق الاستنتاجي، لابد من تحديد أنواع القضايا الحملية أو التصنيفية.

أنواع القضايا الحملية The Four Kinds of Categorical Propositions
هناك أربع أنواع صور نموذجية من القضايا الحملية standard-form categorical propositions ..
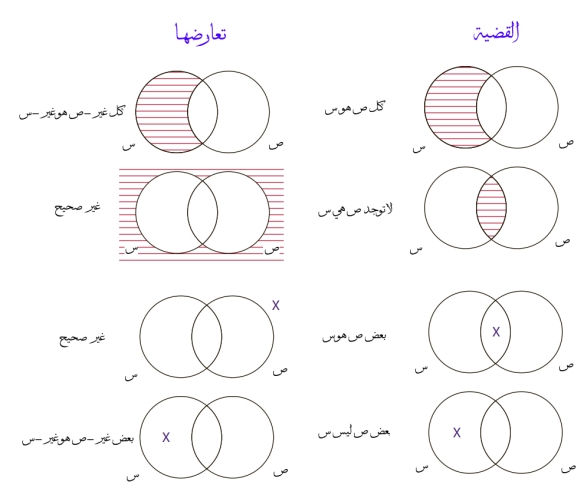
النوع الأول: القضايا الكلية الموجبة (التأكيدية العامة) Universal affirmative propositions وفيها نؤكد حقيقة أن كل أعضاء فئة أو تصنيف ما محتواه أو جزء من فئة او تصنيف آخر .. مثلا “كل السياسيين كاذبين” .. “كل رجال الدين فضلاء” .. “كل رجال الدين فضلاء” .. الخ .. اى ان مثلا كل عضو في فئة او تصنيف السياسين هو أيضا عضو في فئة أو تصنيف الكاذبين. اى ان كل سياسي كاذب .. وبالتالي الايجاب او التأكيد في تلك القضية شامل لكل أعضاء الفئة أى تأكيد كلي عام .. من الممكن صياغة هذا النوع رمزيا كالاتي “كل س هو ص”. حيث س، ص يمثلا اصطلاحي الموضوع Subject والمحمول أو الإسناد Predict .. التأكيد المطروح في هذا النوع يصنع علاقة تضمين او شمول inclusion ما بين فئتين ويقال ان هذة العلاقة كاملة، عامة، أو كلية .. اى ان كل ما في س متضمن في ص .. علماء المنطق يطلقون على هذا النوع من القضايا قضايا A ونرمز لها بقضايا ك-م . القضايا الحملية عادة ما يتم تمثيلها من خلال المخططات كي يسهل دراستها وفهمها، أهم تلك الصور هى استخدام دوائر متقاطعة لتمثيل الفئات وعلاقتها ببعضها البعض، يطلق عليها مخططات فيين Venn diagrams نسبة إلى مخترعها عالم الرياضيات والمنطقي الإنجليزي جون فين John Venn . هذة المخططات تساعد جدا في فهم القضايا الحملية والتحقق من صلاحيتها، وهي شائعة جدا في الرياضيات وعلوم الحوسبة. على اى حال سنرسم دائرتين متقاطعتين، الأولى هي دائرة الموضوع Subject ونرمز لها ب س .. والدائرة الاخرى هي دائرة المحمول أو الإسناد Predict ونرمز لها بـ ص .. في مخطط A ك-م او القضايا الكلية الموجبة نريد إثبات أن كل س هو ص .. وبالتالي تظهر الجزء من دائرة س الخارج على دائرة ص مخطط او مظلل، اى ان لاتوجد به أى عناصر، اى ان لا توجد أي عناصر في الدائرة س ليست جزء من ص (أنظر الشكل المرافق).

النوع الثاني: القضايا الكلية السالبة (النفي العام) Universal negative propositions وفيها ينفي حقيقة أن كل أعضاء فئة ما محتواة في فئة أخرى .. مثلا “لا يوجد سياسي كاذب” .. “لا يوجد رجل دين فاضل” .. “لا يوجد طبيب رحيم” … الخ .. ادعاء ان لايوجد رجل دين فاضل، يصنع علاقة نفي بين فئة رجال الدين وفئة الفضلاء. هذه العلاقة علاقة نفي، وهي ايضا علاقة كاملة، عامة، وكلية .. اى تنطبق على كل أعضاء فئة رجال الدين .. اى ان اعضاء فئة الموضوع س من يستبعدوا بالكامل من فئة المحمول أو الاسناد ص.. من الممكن التعبير عن هذا النوع رمزيا كالاتي “لايوجد س ص” حيث س و ص هما اصطلاحي الموضوع والإسناد. هذة القضية تنفي تماما علاقة التضمين او الانتماء ما بين اصطلاحين. اى لايوجد اى عضو في س ينتمي لـ ص. علماء المنطق يرمز لهذا النوع بقضايا E ونرمز لها ب ك-س .. مخطط فين لقضايا E يمثل الاستبعاد المتبادل mutual exclusion بين فئتين كالاتي برسم دائرتين س و ص متقاطعتين والجزء المتقاطع بينهم مخطط او مظلل، ليعبر عن أنه لا يوجد اى عناصر مشتركة بين الفئتين (أنظر الشكل المرافق).

النوع الثالث: القضايا الجزئية الموجبة (التأكيد الجزئي) Particular affirmative propositions فيها نؤكد حقيقة ان بعض اعضاء فئة ما محتواة في فئة أخرى .. مثلا “بعض السياسيين كاذبين” .. “بعض رجال الدين فاضلين” .. “بعض الأطباء رحماء” .. الخ … اى ان في ادعاء بعض الأطباء رحماء ، نؤكد أن هناك بعض الأطباء رحماء والبعض الآخر غير رحيم. هذا التأكيد شبية بقضايا الكلية الموجبة لكنة غير مطلق أو غير عام، او غير كلي. أى لا ينطبق على كل أعضاء الفئة. فقط على جزء محدد منها. من الممكن قراءة هذه الجملة على ان فئتي الاطباء والفضلاء لديهم بعض الاعضاء المشتركين. لكن “بعض” مصطلح غير محدد او معين. هل نعني به “واحد”، “اثنين”، “ثلاثه”، أو أكثر .. ماهو عدد “البعض”؟ .. علماء المنطق بعدوا عن الالتباس والغموض اللغوى وحددوا البعض على انه “على الاقل عنصر واحد” … من الممكن صياغة قضايا التأكيد المحددة رمزيا كالاتي “بعض س هو ص” .. الذي يعني ان على الاقل هناك عضو واحد في فئة الموضوع س ينتمي أيضا إلى فئة الاسناد ص. وبالتالي هذا النوع يؤكد العلاقة الضمنية بين فئتين لكن فقط جزئيا. أى أن هناك أعضاء محددة مشتركة بين الفئتين، علماء المنطق يرمزوا لهذا النوع بقضايا I أو ج-م. ويمثل بمخطط فين بدائرتين س و ص متقاطعين وعلامة او نقطة واحدة في الجزء المتقاطع لتعبر عن تأكيد أن هناك على الأقل عنصر واحد مشترك بين الفئتين (أنظر الشكل المرافق).
النوع الرابع: القضايا الجزئية السالبة (النفي الجزئي) Particular negative propositions وفيها نؤكد حقيقة أن بعض أعضاء فئة ما ليسوا جزء من فئة أخرى … مثلا “بعض السياسيين ليسوا كاذبين” … “بعض رجال الدين ليسوا فاضلين” .. “بعض الأطباء ليسوا رحماء” .. الخ .. كما في النوع الثالث، هذا النوع لايدعي حقيقة حول كل أعضاء الفئة لكن بعضها، أو بالاصح ينفي حقيقة ما عن بعض أعضاء الفئة بشكل جزئي، ولهذا يطلق على هذا النوع محدد لكن بدلا من التأكيد ينفي! .. من الممكن التعبير عن هذا النوع رمزيا كالاتي “بعض س ليس ص”. وبنفس الصورة التى عبرنا بها عن مصطلح “بعض” يعنى “على الاقل عضو واحد” في فئة الموضوع س يستبعد من فئة الاسناد ص. هذا الاستبعاد جزئي وليس كلي. علماء المنطق يرمزوا لهذا النوع بقضايا O أو ج-س … ومن الممكن التعبير عنها بمخطط فين به دائرتين متقاطعتين س و ص و علامة أو نقطة داخل الجزء في س الغير متقاطع مع ص، للإشارة لحقيقة أن هناك على الأقل عنصر واحد في س لايقع داخل ص (أنظر الشكل المرافق).

هذه الصور الأربعة من قضايا التصنيفات A, E, I, O هي وحدات البناء الأساسية للحجج الاستنتاجية. وأعتقد أن الكثير من المستمعين قد يشعر ان هذه التصنيفات الأربعة بسيطة جدا ومباشرة، وده صحيح، لكن اكتشاف هذه الانواع الاربعة وتحديدها بشكل منهجي من آلاف السنين كان خطوة أساسية هامة في عملية تطور علم المنطق بشكل منهجي. وكانت أحد مساهمات أرسطو الباقية حتى اللحظة في المعرفة الانسانية. لكن هذة البساطة الظاهرة قد تكون خادعة. فوق تلك المنظومة البسيطة من الفئات وتصنيف العلاقات بين الفئات بنى علماء المنطق عبر العصور أنظمة غاية في التعقيد لصياغة وتحليل الحجج الاستنتاجية، كما سنرى بعد قليل، الأمر الذي جعل المنظومة أحد أهم إنجازات العقل البشري إطلاقا.

مخططات فيين Venn Diagrams
عالم المنطق، الفيلسوف و الرياضي الإنجليزي جورج بولي George Boole عُرف بعملة الاهم وهو  تطوير منظومة جبر بول Boolean algebra التي ابتكرها وقدّمها في كتابِه الأوّل تحليل الرياضيات المنطقيّة (The Mathematical Analysis of Logic) عام 1847، وشرحها أكثر ووضع أُسسها في كتابِه استقراء قوانين التفكير (An Investigation of the Laws of Thought) عام . 1854. الجبر البوليني أحد أهم فروع الجبر من حيثُ أهميته في عالم الحوسبة ومنظومة المعلومات الحديثة، لكنة أيضا أحد أهم طرق الوصول للحقيقة حيث يعمل من خلال مُتغيّرين اثنين هما الصح أو الخطأ ويُرمز لهما بالعددين 1 و 0 بعكس الجبر الإبتدائي الذي قد يكون المُتغيّر فيه أي عددٍ كان. الفيلسوف وعالم المنطق الأمريكي Charles Sanders Peirce كان مفتون بفكرة بولي ومنظومته الجبرية، ورأي أن
تطوير منظومة جبر بول Boolean algebra التي ابتكرها وقدّمها في كتابِه الأوّل تحليل الرياضيات المنطقيّة (The Mathematical Analysis of Logic) عام 1847، وشرحها أكثر ووضع أُسسها في كتابِه استقراء قوانين التفكير (An Investigation of the Laws of Thought) عام . 1854. الجبر البوليني أحد أهم فروع الجبر من حيثُ أهميته في عالم الحوسبة ومنظومة المعلومات الحديثة، لكنة أيضا أحد أهم طرق الوصول للحقيقة حيث يعمل من خلال مُتغيّرين اثنين هما الصح أو الخطأ ويُرمز لهما بالعددين 1 و 0 بعكس الجبر الإبتدائي الذي قد يكون المُتغيّر فيه أي عددٍ كان. الفيلسوف وعالم المنطق الأمريكي Charles Sanders Peirce كان مفتون بفكرة بولي ومنظومته الجبرية، ورأي أن  من الممكن استخدامها في تطبيقات في الدوائر الكهربائية، وبالفعل بعد خمسين سنة المهندس والرياضي الأمريكي Claude Shannon وضع النظرية محل التطبيق وصمم منظومة بولينية من الممكن استخدامها في مفاتيح توجيهه التليفونات. هذا الابتكار أدى لاحقًا إلى تطوير أجهزة الكمبيوتر الرقمية الإلكترونية كما نعرفها الآن. قصة بولي وأفكاره الثورية في العلاقة بين الرياضيات والمنطق مثيرة للغاية وسنعود لتفاصيلها مرة أخرى في سلسلة فلسفة الرياضيات Philosophy of Mathematics. على أى حال، من وجهة نظر بولي الاربع انواع من القضايا الحملية يمكن قرائتها كالآتي
من الممكن استخدامها في تطبيقات في الدوائر الكهربائية، وبالفعل بعد خمسين سنة المهندس والرياضي الأمريكي Claude Shannon وضع النظرية محل التطبيق وصمم منظومة بولينية من الممكن استخدامها في مفاتيح توجيهه التليفونات. هذا الابتكار أدى لاحقًا إلى تطوير أجهزة الكمبيوتر الرقمية الإلكترونية كما نعرفها الآن. قصة بولي وأفكاره الثورية في العلاقة بين الرياضيات والمنطق مثيرة للغاية وسنعود لتفاصيلها مرة أخرى في سلسلة فلسفة الرياضيات Philosophy of Mathematics. على أى حال، من وجهة نظر بولي الاربع انواع من القضايا الحملية يمكن قرائتها كالآتي
(1) “كل س هو ص” تساوي لايوجد اي عنصر في س خارج ص
(2) “لا يوجد س هو ص” تساوي لا يوجد عنصر من س داخل ص
(3) “بعض س هو ص” تساوي على الأقل يوجد عنصر واحد من س داخل ص
(4) “بعض س ليس ص” تساوي على الأقل يوجد عنصر واحد من س لا ينتمي لص.
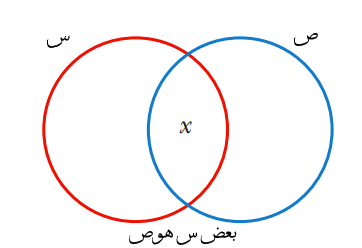
بدمج هذا التفسير مع منظومة مخطوطات فين التى طورها عالم المنطق الانجليزي جون فين John Venn في القرن التاسع عشر، والتي أصبحت معروفة بمخططات فيين Venn diagrams. في منظومة المخطوطات كل فئة يتم تمثيلها بدائرة، إذن القضايا التصنيفية في مخطوطات فين يتم تمثيلها بدائرتين لان دائما هناك فئتين، والعلاقة بين هذين الدائرتين تمثل نوع القضية التصنيفية محل التمثيل. كل دائرة يتم وضع رمز داخلها لاسم الفئة التى تشير إليها. تأمل مثلا “فئة س تمثل كل المصريين” وفئة ص “تمثل كل العمال” .. لو رسمنا مخطط فين فيه دائرة س تتقاطع مع دائرة ص في منقطة نرمز لها ب X .. وكل شئ خارج الدائرتين نرمز له ب O (انظر الشكل المرافق) .. في تلك الحالة الدائرة س ما عدا المنطقة x تمثل كل المصريين باستثناء العمال .. والدائرة ص ما عدا المنطقة x تمثل كل العمال باستثناء العمال المصريين. وتقاطع الدائرة س وص اى المنطقة X تمثل كل العمال المصريين، واخيرا المنطقة المحيطة بالدائرتين O أى شئ يقع في تلك المنطقة لا ينتمي لفئة العمال ولا لفئة المصريين. هذه المنظومة البسيطة من مخططات فين من الممكن تطويرها قليلا كي تستخدم بكفاءة في تمثيل منطق القضايا الحملية. بإضافة رمزين آخرين .. بوضع علامة X داخل منطقة ما هذا يمثل دائما فكرة الوجود، اى أن يوجد على الأقل عنصر واحد في تلك المنطقة، هذا الرمز إذن يستخدم لتمثيل القضايا الحملية الجزئية I and O وعند تظليل منطقة يشير هذا دائما الى الفراغ اى ان لايوجد اى عناصر في تلك المنطقة، وبالتالي يساعد هذا في تمثيل القضايا الحملية الكلية A and E.
.. في تلك الحالة الدائرة س ما عدا المنطقة x تمثل كل المصريين باستثناء العمال .. والدائرة ص ما عدا المنطقة x تمثل كل العمال باستثناء العمال المصريين. وتقاطع الدائرة س وص اى المنطقة X تمثل كل العمال المصريين، واخيرا المنطقة المحيطة بالدائرتين O أى شئ يقع في تلك المنطقة لا ينتمي لفئة العمال ولا لفئة المصريين. هذه المنظومة البسيطة من مخططات فين من الممكن تطويرها قليلا كي تستخدم بكفاءة في تمثيل منطق القضايا الحملية. بإضافة رمزين آخرين .. بوضع علامة X داخل منطقة ما هذا يمثل دائما فكرة الوجود، اى أن يوجد على الأقل عنصر واحد في تلك المنطقة، هذا الرمز إذن يستخدم لتمثيل القضايا الحملية الجزئية I and O وعند تظليل منطقة يشير هذا دائما الى الفراغ اى ان لايوجد اى عناصر في تلك المنطقة، وبالتالي يساعد هذا في تمثيل القضايا الحملية الكلية A and E.

تشريح القضايا الحملية Dissecting Categorical Propositions

القضايا الحملية في أيا من صورها الاربعة النموذجية لها مكونات أربعة أساسية
(1) الموضوع وهو ما نحكم عليه بالايجاب أو السلب في القضية Subject.
(2) المحمول أو الإسناد وهو ما نحكم به إيجابا أو سلبا على الموضوع Predicate
(3 ) المعامل Quantifier إن كان الحكم كلي عام على كل أعضاء الفئة او جزئي محدد على بعض أعضاء فئة الموضوع يتم تحديدة من خلال المعامل
(4) وأخيرا الرابط Copula هو المعامل اللغوي المستخدم لربط الحمل والاسناد بالموضوع.
مثلا في القضية التصنيفية الشهيرة “كل إنسان فان” .. “كل” هي المعامل وفي هذه الحالة المعامل يشير الى قضية كلية عامة ، أما الموضوع هو “إنسان” ، والمحمول أو المسند هو “فان”، وأخيرا الرابط غائب في تلك الجملة لأنه غير مطلوب لغويا. علماء المنطق اعتادوا على تقسيم القضايا الحملية إلى قسمين، الأول تقسيم من حيث الكيف Quality والثاني تقسيم من حيث الكم Quantity. كل صورة من القضايا الحملية في قالبها القياسي أما تؤكد او تنفي علاقة فئوية ما. لو أكد الادعاء علاقة تضمينية ما بين فئتين سواء بصورة كلية أو جزئية في تلك الحالة يقال أن الخاصية الكيفية للقضية Quality هي التأكيد أو الإيجاب affirmative. إذن القضايا من نوع A ك-م “كل س هو ص” والقضايا من نوع I ج-م ” بعض س هو ص” الخاصية الكيفية لكليهما هي التأكيد أو الإيجاب. أو ان نفي الادعاء علاقة تضمينية ما بين فئتين سواء بصورة كلية أو جزئية في تلك الحالة يقال أن الخاصية الكيفية للقضية هي النفي أو السلب negative ، إذن القضايا من نوع E ك-س “لا يوجد اى س هو ص” و القضايا من نوع O ج-س “بعض س ليس ص” الخاصية الكيفية لكليهما هي النفي أو السلب. كل قضية حملية كما هو بديهي بالنسبة لك تمتلك خاصية كيفية واحدة إما إيجاب أو سلب. وبنفس الصورة كل قضية حملية في صورتها القياسية لها خاصية كمية Quantity واحدة فقط، إن كانت القضية تشير الى كافة عناصر فئة الموضوع في تلك الحالة يقال أن الخاصية الكمية للقضية عامة أو كلية universal ، وبالتالي القضايا التصنيفية من نوع A ك-م “كل س هو ص” والقضايا من نوع E ك-س “لايوجد س هو ص” يمتلك خاصية كمية عامة. لكن لو كانت القضايا تشير الى بعض عناصر فئة الموضوع، في تلك الحالة الخاصية الكمية للقضية تكون جزئية particular . وبالتالي القضايا من نوع I ج-م “بعض س هو ص” والقضايا من نوع O ج-س “بعض س ليس ص” يمتلكا خاصية كمية جزئية. الخاصية الكمية في الشكل القياسي للقضايا الحملية يمكن التعرف عليه بسهولة من خلال الكلمات المفتاحية “كل”، “ليس”، تشير للقضايا العامة .. و”بعض” تشير الى القضايا المحددة. إذن كل قضية حملية لها خاصية كيفية واحدة إما إيجاب أو سلب وخاصية كمية واحدة إما كلية أو جزئية ، وبالتالي الانواع الاربعة التى وضعها أرسطو في تصنيفه للقضايا الحملية. بين فئة الموضوع وفئة الإسناد أو المحمول في كل قضية حملية في شكلها القياسي يوجد رابط لغوي مثلا كل س هو ص في تلك الحالة الرابط “هو” .. يطلق على هذا المعامل “الرابط copula” .. معامل الربط قد يظهر في صور وأشكال عديدة حسب سياق الجملة .. مثلا “بعض الملوك كانوا سفاحين” .. “كانوا” في تلك الحالة هو معامل الربط. هناك خاصية هامة جدا في القضايا الحملية وهي خاصية التوزيع distribution. القضية توزع فئة ما إذا اشارات الى كافة عناصر تلك الفئة. علي سبيل المثال “كل السياسين بشر” معامل الكمية “كل” في تلك الحالة يشير الى كل عناصر فئة الموضوع “السياسيين” لكنه لا يشير الى عناصر فئة البشر. اى ان القضية تؤكد أن كل السياسيين من البشر لكن لا تقر اى شئ حول الاتجاه المعاكس للقضية وهو أن كل عناصر فئة البشر من السياسيين. اى ان القضية وزعت فئة السياسيين على فئة البشر وليس العكس. في قضايا الكلية الموجية A ك-م، فئة الموضوع يتم توزيعها لكن فئة الإسناد أو المحمول لايتم توزيعها. في قضايا الكلية السلبية E ك-س مثلا “لا يوجد كاتب جاهل” فئة الموضوع “الكتاب” تم توزيعها لأن فئة الكتاب بالكامل تم استبعادها من فئة الجهل. لكن ايضا فئة الجهلاء تم استبعاد كافة عناصرها بالكامل من فئة الكتاب، اى ان لايوجد جاهل أيضا كاتب والعكس بالعكس، إذن على النقيض من قضايا الكلية الموجبة، قضايا الكلية السالبة توزع كلا من فئة الموضوع والمحمول في كلا الاتجاهين. في قضايا الجزئية الموجبة I ج-م .. مثلا “بعض الجنود خونة” التأكيد لم يتم صنعة حول كل الجنود، وايضا لم تصنع أي تأكيد حول كل الخونة. اى ان القضية لا تدعي شئ حول كل جندى أو حول كل خائن. اى ان ايا من الفئتين لم يتم تأكيدهم أو استبعادهم بشكل عام او كلي من الاخرى. وبالتالي يقال ان في القضايا الجزئية الموجية كلا من فئة الموضوع وفئة المحمول غير قابلة للتوزيع undistributed. واخيرا قضايا الجزئية السالبة O ج-س مثلا “بعض الكلاب ليست أليفة” .. القضية لا تدعي شئ حول كل الكلاب، فقط الى بعض الكلاب، أو بعض عناصر الفئة، اى تدعي أن هذا الجزء المحدد من فئة الكلاب يستبعد من فئة كل الكائنات الاليفة، لكن القضية تدعي أن كافة عناصر فئة المحمول تُستبعد بالكامل من الجزء المحدد من فئة الموضوع، اى ان لا توجد كائنات أليفة في هذا الجزء من فئة الكلاب. وبالتالي قضايا الجزئية السلبية فيها فئة الموضوع غير قابلة للتوزيع لكن فئة المحمول موزعة. إذن كلا من قضايا الإيجاب والسلب العام توزع فئة الموضع، لكن قضايا الايجاب و السلب الجزئي لاتوزع فئة الموضوع، اى بصورة أخرى معامل الكمي quantity في القضية يحدد إن كانت فئة الموضوع سيتم توزيعها أم لا. و بنفس الصورة قضايا الكلية الموجبة و الجزئية لا توزع فئة المحمول، في حين أن كلا من قضايا السلب الكلي و الجزئي توزع فئة المحمول. إذن معامل الكيف quality يحدد إن كانت فئة المحمول قابلة للتوزيع ام لا. بتبسيط غير مخل، قضايا الكلية الموجبة A ك-م توزع فقط فئة المحمول. ـ قضايا الكلية السالبة E ك-س توزع كلا من فئة الموضوع والمحمول، وقضايا الجزئية الموجبة I ج-م لاتوزع أيا من الفئتين، وأخيرا قضايا الجزئية السالبة O ج-س توزع فقط فئة المحمول (أنظر الشكل المرافق)، فهم هذه الخواص وتأثيرها علي صور القضايا الحملية القياسية سيصبح جوهرى عند تقييم وتحليل حجج القياس المنطقي syllogisms .
اى ان لايوجد جاهل أيضا كاتب والعكس بالعكس، إذن على النقيض من قضايا الكلية الموجبة، قضايا الكلية السالبة توزع كلا من فئة الموضوع والمحمول في كلا الاتجاهين. في قضايا الجزئية الموجبة I ج-م .. مثلا “بعض الجنود خونة” التأكيد لم يتم صنعة حول كل الجنود، وايضا لم تصنع أي تأكيد حول كل الخونة. اى ان القضية لا تدعي شئ حول كل جندى أو حول كل خائن. اى ان ايا من الفئتين لم يتم تأكيدهم أو استبعادهم بشكل عام او كلي من الاخرى. وبالتالي يقال ان في القضايا الجزئية الموجية كلا من فئة الموضوع وفئة المحمول غير قابلة للتوزيع undistributed. واخيرا قضايا الجزئية السالبة O ج-س مثلا “بعض الكلاب ليست أليفة” .. القضية لا تدعي شئ حول كل الكلاب، فقط الى بعض الكلاب، أو بعض عناصر الفئة، اى تدعي أن هذا الجزء المحدد من فئة الكلاب يستبعد من فئة كل الكائنات الاليفة، لكن القضية تدعي أن كافة عناصر فئة المحمول تُستبعد بالكامل من الجزء المحدد من فئة الموضوع، اى ان لا توجد كائنات أليفة في هذا الجزء من فئة الكلاب. وبالتالي قضايا الجزئية السلبية فيها فئة الموضوع غير قابلة للتوزيع لكن فئة المحمول موزعة. إذن كلا من قضايا الإيجاب والسلب العام توزع فئة الموضع، لكن قضايا الايجاب و السلب الجزئي لاتوزع فئة الموضوع، اى بصورة أخرى معامل الكمي quantity في القضية يحدد إن كانت فئة الموضوع سيتم توزيعها أم لا. و بنفس الصورة قضايا الكلية الموجبة و الجزئية لا توزع فئة المحمول، في حين أن كلا من قضايا السلب الكلي و الجزئي توزع فئة المحمول. إذن معامل الكيف quality يحدد إن كانت فئة المحمول قابلة للتوزيع ام لا. بتبسيط غير مخل، قضايا الكلية الموجبة A ك-م توزع فقط فئة المحمول. ـ قضايا الكلية السالبة E ك-س توزع كلا من فئة الموضوع والمحمول، وقضايا الجزئية الموجبة I ج-م لاتوزع أيا من الفئتين، وأخيرا قضايا الجزئية السالبة O ج-س توزع فقط فئة المحمول (أنظر الشكل المرافق)، فهم هذه الخواص وتأثيرها علي صور القضايا الحملية القياسية سيصبح جوهرى عند تقييم وتحليل حجج القياس المنطقي syllogisms .

مربع ارسطو The Traditional Square of Opposition
الاستدلال هو الموضوع الرئيسي في الدراسات المنطقية، في المنطق الكلاسيكي الذي بدأ على أيد أرسطو ولذا يطلق عليه المنطق الأرسطي، أهتم فيه أرسطو بصورتين أساسيتين الاستدلال المباشر و الاستدلال الغير مباشر، القضايا الحملية في صورتها النموذجية، رأينا ان هناك شقين او فئتين للقضية، فئة الموضوع وفئة المحمول، الفئتين قد يختلفا من قضية لأخرى في الكيف أو الكم، او كليهما. مثلا هناك قضايا كلية موجبة وأخرى كلية سلبية، وهناك قضايا جزئية موجبة وأخرى جزئية سلبية. الاصطلاح التقني الذي يطلق على هذا الاختلاف بين القضايا يطلق عليه التقابل opposition. عملية التشريح التى قمنا بها منذ قليل لمكونات ومعاملات القضايا التصنيفية ستصبح هامة جدا الان عند محاول فهم صور هذا التقابل بين القضايا وتحويل عملية البحث عن الحقيقة الى معادلة رياضية يقينية. في عملية الاستدلال المباشر نبحث عن كيفية استنتاج صدق او كذب قضية من خلال معرفتنا بحقيقة قضية أخرى متفقة أو مختلفة معها كماٌ، كيفاُ، أو كليهما. هذة العلاقة بين القضيتين يتم صياغتها وفق مجموعة من القوانين. هناك عدة صور من التقابل في القضايا الحملية ترتبط بشكل وثيق مع حقيقة القضية محل الدراسة.

النوع الأول: التقابل بالتضاد Contraries
قضيتين يقال إنهما متضادتين إن كان من غير الممكن أن تكون كلاهما صحيحة، أي أن حقيقة إحداهما تستبع خطأ الأخرى .. مثلا “فريق الأهلي سيكسب المباراة القادمة مع الزمالك” قضية في حالة تضاد مع “فريق الزمالك سيكسب المباراة القادمة مع الأهلي”. طبعا ان كانت القضيتين يشيرا الى نفس المباراة. إن كانت إحداهما صحيحة لابد وأن تكون الثانية خاطئة. لكن هاتين القضيتين لا يوجد بينهم تناقض contradiction ، لان المباراة قد تنتهي بالتعادل وفي تلك الحالة كلا القضيتين يصبحا خاطئتين. في التضاد Contrary كلا القضيتين لا يمكن أن يكونا صحيحين لكن على العكس من التناقض contradiction، القضيتين قد يكونا خاطئين. في قواعد التحليل المنطقي الأرسطي او الكلاسيكي، عادة ما تم النظر الى القضايا العامة على أنها في حالة تضاد، الكلية الموجبة A ك-م و الكلية السلبية E ك-س المشتركين في فئة الموضوع وفئة المحمول لهما نفس معامل الكم الكلي لكن يختلفا في معامل الكيف(إحداهما إيجاب والأخرى سلب) مثلا “كل المغنين عاطفين” و “لا يوجد مغني عاطفي” لا يمكن أن يكونا صحيحتين في نفس الوقت، لكن كليهما من الممكن أن يكونا خاطئتين وفي تلك الحالة يعتبرا متضادتين. لكن هذا التحليل الأرسطي تشوبه بعض الإشكاليات سنناقشها بعد قليل. احد الاشكاليات التي يواجهها هذا التحليل، عندما تكون حقيقية إحدى القضيتين حقيقة ضرورية، او حقيقة منطقية أو رياضية. مثلا “كل المربعات مستطيلات” و “لا توجد مربعات دوائر” … في تلك الحالة ادعاء أن قضية الكلية الموجبة A ك-م وقضية الكلية السلبية E ك-س متضادتين لا يمكن أن يكونا صحيحتين. لأن حقيقة ضرورية لا يوجد اي احتمال ان تكون خاطئة، وبالتالي لا يمكن أن يكون هناك اى قضية مضادة لها، لو الفكرة غريبة عليك فكر في “المربعات ليست دوائر” جملة حقيقتها ضرورية لا يمكن أن تكون خاطئة، وبالتالي لا يمكن أن يكون هناك أى قضية أخرى مضادة لها، القضايا التى حقيقتها أو خطئها ليس ضروريا يطلق عليها المشروطات Contingent ولهذا في التحليل الأرسطي يتم اعتبار ان القضايا المتضادة قضايا مشروطة اى ان حقيقتها ليست ضرورية.
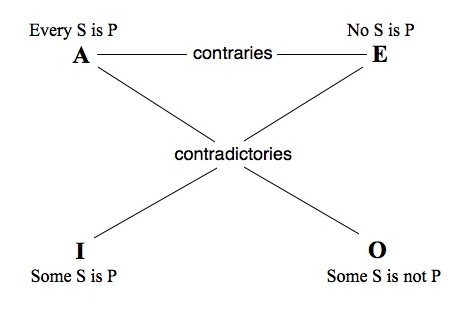
النوع الثاني: التقابل بالتناقض Contradictories
قضيتين يعدا متقابلتين بالتناقض إن كانت إحداهما تنفي الاخرى، اى ان كان من المستحيل أن يكون كلاهما صحيحتان أو خاطئتين في نفس الوقت. قضيتين حول نفس فئة الموضوع والمحمول ولكن يختلفا في كلا من الكيف والكم هو صورة من التقابل بالتناقض. أى أن القضايا الكلية الموجبة A ك-م مثلا “كل القضاة درسوا القانون” .. و القضايا الجزئية السلبية O ج-س “بعض القضاة لم يدرسوا القانون” .. يعدا قضيتين متقابلتين بالتناقض! .. اى ان لا يمكن أن يكونا صحيحتين في نفس الوقت. هذا لان هناك اختلاف في معامل الكيف بينهما (أحدهما ايجاب والاخرى سلب) ، وهناك ايضا اختلاف في معامل الكم (أحدهما كلية عامة، والاخرى جزئية محددة) . إذن لابد أن إحداهما صحيحة والأخرى خاطئة. وبنفس الصورة قضايا الكلية الموجبة E ك-س وقضايا الجزئية الموجبة I ج-م يعد تقابل بالتناقض”لايوجد س هو ص” في مقابل “بعض س هو ص”.

النوع الثالث: التقابل بالدخول تحت التضاد Subcontraries
قضيتين يقال انهما في حالة تقابل بالدخول تحت التضاد لو كان من غير الممكن أن يكونا خاطئتين لكن من الجائز أن يكونا صحيحتين في نفس الوقت. في التحليل الأرسطي الكلاسيكي القضايا الجزئية الموجبة والسالبة في حالة تقابل بالدخول تحت التضاد، لهما نفس الموضوع والمحمول، ونفس الكمية لكن يختلفا في معامل الكم أحدهما موجب يأكد والآخر سالب ينفي. مثلا قضية جزئي موجب I ج-م “بعض الماس من الأحجار الكريمة” .. و قضية جزئية سالبة O ج-س”بعض الماس ليس من الأحجار الكريمة” .. كلا الجملتين من الممكن أن يكونا صحيحين لكن من غير الممكن أن يكون كليهما خاطئتين، ولهذا يطلق عليهم تقابل بالدخول تحت التضاد. لكن بنفس الصورة في حالة التقابل بالتناقض، هناك بعض الصعوبات المنطقية التي تظهر في هذا التحليل، لو كانت القضايا من نوع I أو O خاطئة بالضرورة مثلا “بعض المربعات دوائر” أو “بعض المربعات ليست مستطيلات” .. لا يمكن أن يكون هناك تقابل بالدخول تحت التضاد مع تلك القضايا، لأن قضيتين في حالة تقابل بالدخول تحت التضاد من الممكن أن يكونا صحيحين، لكن لو كلا القضيتين خاطئتين بالضرورة إذن من المستحيل أن يكون كلاهما صحيحتان في نفس الوقت! .. إذن بنفس الصورة السابقة، التقابل بالدخول تحت التضاد من الممكن أن يحدث فقط طبقا للتحليل الأرسطي الكلاسيكي بين القضايا المشروطة وليست الضرورية.
النوع الرابع: التقابل بالتداخل subalternation
عندما يكون هناك قضيتين حول نفس فئة الموضوع وفئة المحمول، يتفقا في معامل الكيف (اى كلاهما موجب او سالب) .. لكن يختلفا في الكمية (احداهما كلية والاخرى جزئية) .. في تلك الحالة يطلق عليهم القضايا المتداخلة corresponding propositions هذا ايضا يصنف كنوع من التقابل opposition بالرغم من أنه لا يوجد تعارض بالمعنى الحرفي لكنه تصنيفي في تلك الحالة. لهذا قضايا الكلية الموجبة A ك-م “كل الحشرات تطير” تقابلها بالتداخل قضية جزئية موجبة l ج-م “بعض الحشرات تطير” .. وبنفس الصورة قضايا الكلية السالبة E ك-س ” لا يوجد حيتان من الأسماك” .. تقابلها بالتداخل جملة جزئية سالبة O ج-س “بعض الحيتان ليست من الاسماك” .. هذا التقابل بالتداخل بين القضايا الكلية، ومقابلتها من القضايا الجزئية يعرف التقابل بالتداخل subalternation في هذا النوع من التقابل، القضية الكلية يطلق عليها البدل superaltern والقضية المحددة أو الجزئية يطلق عليها تابع البدل subaltern … حقيقة البدل تدل على حقيقة تابع البدل، مثلا من قضية كلية موجبة “كل الطيور لديها ريش” .. بدل يدل على حقيقة تابع البدل القضية الجزئية الموجبة “بعض الطيور لديها ريش” .. و قضية كلية موجبة “لا توجد حيتان من الأسماك” .. بدل يدل على حقيقة تابع البدل قضية جزئية سالبة “بعض الحيتان ليست من الاسماك” … لكن العكس غير صحيح، أي أن حقيقة تابع البدل اى القضايا الجزئية لا تدل على حقيقة البدل نفسة اى القضايا الكلية، مثلا “بعض الحيوانات كلاب” لا يتبع منها ان “كل الحيوانات كلاب” .. و في حالة النفي “بعض الحيوانات ليست كلاب” لا تدل على حقيقة “لا يوجد حيوانات كلاب”!

إذن هناك أربع طرق مختلفة من الممكن أن يحدث بيها التقابل بين القضايا الحملية التناقض contradictories، التضاد contraries ، الدخول تحت التضاد subcontraries ، والتداخل subalternation. علماء المنطلق وضعوا هذه العلاقات في مخطط يطلقوا عليه مربع التقابل The Square of Opposition وعرف تاريخيا بمربع أرسطو (أنظر الشكل المرافق) .. العلاقات بين القضايا في هذا المخطط لمئات السنين أعتقد أنها كافية لتشكيل الاساس المنطقي للتأكد من صلاحية الحجج المنطقية. لأن هناك استدلالات فورية من الممكن ان نصل اليها بمجرد تطبيق قواعد مربع التقابل. مثلا في حالة قضية كلية موجبة A ك-م من الممكن أن نستدل بشكل مباشر أن قضية جزئية سالبة O ج-س لابد وأن تكون خاطئة، و القضية الجزئية الموجبة ج-م لابد وان تكون صحيحة، وهكذا. أي أن بداية بحقيقة او خطأ أي من القضايا الحملية في صورتها القياسية حقيقة او خطأ بعض او كل الصور الأخرى من الممكن أن يستدل عليه بشكل مباشر أو شكل غير مباشر .. مثلا قضية كلية موجبة A ك-م حقيقية: تدل على ان القضية الكلية السالبة E ك-س المقابلة لابد وان تكون خاطئة، و قضية جزئية موجبة I ج-م صحيحة، لابد وان تدل على خطأ القضية الجزئية السالبة المقابلة O ج-س. (أنظر الجدول المرافق).

صور أخرى للاستدلال المباشر Further Immediate Inferences
التقابل ليس الصور الوحيدة التى يمكن من خلالها الاستدلال على حقيقة القضايا الحملية بشكل مباشر من قضية أخرى، لكن هناك خواص أخرى تقع تحت نظرية الاستدلال المباشر. تأمل القضية التالية “لا توجد كلاب قطط” .. القضية ببساطة تدعي ان لا يوجد اى تقاطع بين فئة الكلاب و فئة القطط. اى ان فئة الكلاب منفصلة ومستقلة تماما عن فئة القطط. الآن تأمل هذه القضية “لا توجد قطط كلاب” .. هذه القضية تصنع نفس الادعاء. وبالتالي الجملتين لهم نفس المعنى ونفس قيمة الحقيقة. الآن تأمل هذه الجملة “بعض الكلاب ليست مهجنة” هذه الجملة تدعي أن هناك على الأقل كلب واحد يقع خارج فئة الكلاب المهجنة اى انه أصيل المنشأ. و جملة “بعض الكلاب أصيلة المنشأ” تدعي نفس الحقيقة لكن بصورة اخرى. إذن نفس الفكرة، قضيتين لهم نفس المعنى وقيمة الحقيقة. هناك عمليات استدلالية من الممكن أن نجريها على القضايا قد تقود او لا تقود الى قضية اخرى لها نفس المعنى وقيمة الحقيقة.
العكس المستوى Conversion
هو أبسط تلك العمليات وهو عملية نقوم فيها بعكس فئة الموضوع مع فئة المحمول. مثلا “لا يوجد رجال ملائكة” نحولها الي “لا يوجد ملائكة رجال” .. هذه القضايا من الممكن أن يستدل على صلاحيتها من بعضها البعض. مثلا في جملة “لا توجد كلاب من البرمائيات” لو طبقنا عليها عملية العكس المستوى تصبح “لا توجد برمائيات من الكلاب” .. الجملة الناتجة يطلق عليها عكس converse القضية الأولى. عند تطبيق العكس المستوي على الصور الأربعة النموذجية للقضايا الحملية نحصل على الآتي
(1) كل س هو ص .. عكسها .. كل ص هو س
(2) لاتوجد س هي ص .. عكسها .. لا توجد ص هي س
(3) بعض س هو ص .. عكسها .. بعض ص هو س
(4) بعض س ليس ص .. عكسها .. بعض ص ليس س (أنظر الشكل المرافق).
لو تأملت الشكل المرافق لمخطط فين في حالة الكلية السالبة E ك-س ستلاحظ أن المخطط متطابق في حالة العكس المستوى مع الأصل منطقة التقاطع مظللة بين الدائرتين. أي أن الجملة وعكسها متطابقتين منطقيا logically equivalent اى ان لهم نفس المعنى ونفس قيمة الحقيقة. وبنفس الصورة ستجد مخطط فين في قضايا الجزئية الموجبة I ج-م متطابقة، علامة X في منطقة التقاطع بين الدائرتين، اى ان الجملتين متطابقتين منطقيا من حيث المعنى وقيمة الحقيقة. إذن تطبيق عملية العكس المستوي على قضية كلية سالبة E ك-س أو جزئية موجبة I ج-م دائما ما سينتج جملة لها نفس قيمة الحقيقة أو مكافأة منطقيا. لكن على النقيض، مخطط فين لقضايا الكلية الموجبة A ك-م واضح جدا انه غير متطابق مع مخطط القضية الناتجة من العكس المستوى وكذلك مخطط فين لقضايا الجزئية السالبة O ج-س غير متطابق مع مخطط القضية الناتجة عن العكس المستوي. اى ان قضية الكلية الموجبة وعكسها غير مرتبطتين منطقيا بقيمة الحقيقة، وكذلك قضايا الجزئية السالبة وعكسها. بصورة أبسط عكس قضايا A أو O سينتج قضايا جديدة تماما قيمة حقيقتها غير محددة من خلال علاقتها بالقضايا الاساسية التى تم العكس منها. هذة القضايا الناتجة عن التحويل لها قيمة حقيقة طبعا! لكن المنطق وحده غير كافي للتعرف على تلك القيمة. هذه الفكرة هامة جدا، ان كانت قضايا الكلية السالبة E ك-س وقضايا الجزئية الموجبة I ج-م عكسها ينتج قضايا حقيقتها مؤكدة منطقيا ضروريا، إذن من الممكن بناء استدلالات مباشرة على تلك القضايا .. مثلا “لا يوجد س هو ص. اذن، لا يوجد ص هو س” .. أو “بعض س هو ص. إذن، بعض ص هو س” .. وبما أن النتيجة لهذة الاستدلالات حقيقية ضروريا، اى ان قيمة حقيقتها مطابقة للمقدمة، إذن لو كانت المقدمات صحيحة لابد وان تكون النتائج صحيحة. لكن على الجانب الآخر، هذا النوع من الاستدلال خاطئ في حالة قضايا الكلية الموجبة A ك-م وقضايا الجزئية السالبة O ج-س .. مثلا “كل س هو ص. إذن، كل ص هو س” .. أو “بعض س ليس ص. إذن، بعض ص ليس س” .. هذه الاستدلالات يقال انها ارتكبت مغالطة العكس الغير مشروع llicit conversion لأن قيمة الحقيقة للنتيجة ليست ضرورية منطقيا وبالتالي لا يمكن الاستدلال عليها بشكل مباشر. علي سبيل المثال “كل القطط من الحيوانات .. إذن، كل الحيوانات من القطط” .. او “بعض الحيوانات ليست كلاب .. إذن، بعض الكلاب ليست حيوانات!”

الاستدلال بنقض المحمول (التغيير) Obversion
قبل ما أطرح عليك النوع الثاني من عمليات الاستدلال المباشر هناك فكرة منطقية رياضية مهمة جدا حول الفئات تعرف بالفئة المكملة complementary class . الفئة كما رأينا هي مجموعة من العناصر أو الأشياء التي تشترك في مجموعة من الخواص المشتركة المحددة (ارجع لحلقة المعني و المنطق) .. هذة الخواص المشتركة يطلق عليها السمات المميزة للفئة class-defining characteristic .. مثلا فئة البشر هي مجموعة كل العناصر التي تشترك في سمات مميزة للبشر. كل فئة لها فئة أخرى مكملة تعرف بالفئة المكملة complementary وهي مجموعة كل العناصر او الاشياء التى لا تنتمي للفئة الاصلية. اى ان الفئة المكملة لفئة البشر هي مجموعة العناصر التي ليست من البشر. السمات المميزة للفئة المكملة هي نفي الصفات المكملة للفئة الأصلية، اى ان الفئة المكملة للبشر هي العناصر التي تشترك في نفي الصفات البشرية .. الحيوانات، السيارات، الجبال، الفواكه، الخ. لكن ليست فئة الاطباء، لان الاطباء بشر .. في المنطق عادة ما يضاف معامل نفي أمام رمز الفئة للإشارة لانها فئة مكملة .. مثلا الفئة س .. مكملها هو ليس-س أو غير-س. العلاقة بين الفئة والفئة المكملة من الممكن تمثيلها بمخططات فين في صورة دائرة للفئة، وكل شئ خارج الدائرة هو مكمل الفئة (انظر الشكل المرافق) هذه المقدمة مهمة لفهم النوع الثاني من عمليات الاستدلال المباشر وهو نقض  المحمول أو التغيير Obversion وهو نوع من الاستدلال المباشر من السهل فهمة بمجرد فهم فكرة المكملات، عملية التغيير أكثر تعقيدا من عملية العكس المستوي. وتتم في خطوتين (1) نقوم بتغيير معامل الكيف Quality لفئة الموضوع دون تغيير معامل الكم Quantity مثلا “لا يوجد س هو ص (تصبح) كل س هو ص” أو “بعض س هو ص (تصبح) بعض س ليس ص” .. (2) نستبدل فئة الإسناد بالفئة المكملة لها. على سبيل المثال “كل الاحصنة من الحيوانات” .. بتطبيق عملية التغيير على القضية السابقة تنتج القضية “لا توجد أحصنة من غير-الحيوانات” أي لا توجد أحصنة ليست من فئة الحيوانات. أو “بعض الأشجار من الصنوبر” .. التغيير يصبح “بعض الأشجار ليست من غير-الصنوبر” .. القضية الناتجة تكافئ القضية الأصل ولكنها أصبحت في صورة نفي مزدوج صورتة “لا … غير … ” والقاعدة المنطقية الرياضية البسيطة هي نفي النفي إثبات، أى ان العملية الاستدلالية المنطقية قادتنا مرة أخرى الى قضيتنا الاصلية. صور القضايا الحملية الاربعة تتغير كالآتي
المحمول أو التغيير Obversion وهو نوع من الاستدلال المباشر من السهل فهمة بمجرد فهم فكرة المكملات، عملية التغيير أكثر تعقيدا من عملية العكس المستوي. وتتم في خطوتين (1) نقوم بتغيير معامل الكيف Quality لفئة الموضوع دون تغيير معامل الكم Quantity مثلا “لا يوجد س هو ص (تصبح) كل س هو ص” أو “بعض س هو ص (تصبح) بعض س ليس ص” .. (2) نستبدل فئة الإسناد بالفئة المكملة لها. على سبيل المثال “كل الاحصنة من الحيوانات” .. بتطبيق عملية التغيير على القضية السابقة تنتج القضية “لا توجد أحصنة من غير-الحيوانات” أي لا توجد أحصنة ليست من فئة الحيوانات. أو “بعض الأشجار من الصنوبر” .. التغيير يصبح “بعض الأشجار ليست من غير-الصنوبر” .. القضية الناتجة تكافئ القضية الأصل ولكنها أصبحت في صورة نفي مزدوج صورتة “لا … غير … ” والقاعدة المنطقية الرياضية البسيطة هي نفي النفي إثبات، أى ان العملية الاستدلالية المنطقية قادتنا مرة أخرى الى قضيتنا الاصلية. صور القضايا الحملية الاربعة تتغير كالآتي
(1) قضية كلية موجبة ك-م كل س هو ص .. تتغير الى قضية كلية سالبة ك-س، لا يوجد س هو غير-ص .. مثلا “كل المواطنين من الناخبين” .. تتغير إلى .. “لا يوجد مواطنين من غير-الناخبين” هاتين القضيتين متكافئتين منطقيا و يمكن اشتقاقهم من بعضهم البعض .. الخطوات بسيطة، غيرنا معامل الكيف من إيجاب لسلب .. واستبدلنا فئة الإسناد “الناخبين” بالفئة المكملة وهي “غير-الناخبين”.
(2) قضية كلية سالبة ك-س “لا يوجد س هو ص” .. تتغير إلى كلية موجبة ك-م .. “كل س هو غير ص” .. مثلا “لا يوجد أطفال متزوجين” .. تتغير إلى .. “كل الأطفال غير-متزوجين”
(3) قضية جزئية موجبة ج-م “بعض س هو ص” .. تتغير إلى جزئية سالبة ج-س .. “بعض س هو ليس غير ص” .. مثلا “بعض المعادن من ناقلات الحرارة” .. تتغير إلى .. “بعض المعادن ليست من غير-ناقلات الحرارة”
(4) قضية جزئية سالبة ج-س “بعض س هو ليس ص” .. تتغير إلى جزئية موجبة ج-م .. “بعض س هو غير-ص” .. مثلا “بعض الدول ليست محاربة” .. تتغير إلى .. “بعض الدول هي من غير غير-المحاربين”.

لو تأملت الشكل المرافق لمخططات فين ستجد ان كل زوج من القضايا وتغيرها المخطط متطابق تماما، اى ان كل القضايا الاربعة متطابقة منطقيا مع القضايا الناتجة عن تطبيق عملية التغيير عليها. أى أن لها نفس المعنى ونفس قيمة الحقيقة. لو قمت بتغيير قضية كلية موجبة A ك-م وكانت لها قيمة حقيقة صواب، إذن الجملة الناتجة ايضا لابد وان تكون لها نفس قيمة الحقيقة أي أنها صواب. وهكذا. وأكيد ستكون قادر على تصور عملية تغيير المُتغير، اى ان لو هناك قضية هي تغيير قضية أصلية، وقمت بتطبيق التغيير مرة أخرى عليها، القضية الناتجة ستصبح الجملة الاصلية مرة أخرى .. او “نفي النفي إثبات” .. مثلا أنقلاب جملة “كل الاحصنة من الحيوانات” .. هو “لا توجد أحصنة من غير-الحيوانات” .. لو حاولت تطبيق التغيير مرة أخرى على الجملة الناتجة .. اولا سنغير معامل الكيف لفئة الموضوع اذن “لا” تستبدل ب “كل” .. و سنغيير فئة الإسناد بمكلمتها، في تلك الحالة مكمل فئة “غير-الحيوانات” هي “الحيوانات” .. إذن ستحصل على “كل الاحصنة من الحيوانات” .. اى انك ستحصل على الجملة الأصلية مرة أخرى!

الاستدلال بالتعارض Contraposition
الصورة الاخرى من عمليات الاستدلال المباشر هي التعارض ، وتتم على خطوتين (1) استبدال فئة الموضوع بفئة المحمول (2) تغيير فئة الموضوع بالفئة المكملة وفئة المحمول بالفئة المكملة لها. مثلا “كل الحمام من الطيور” لو طبقنا عليها عملية التعارض نحصل على “كل غير-الطيور من غير-الحمام” .. الجملة الناتجة يطلق عليها الجملة المعارضة contrapositive. التعارض Contraposition يمكن الوصول إليه من خلال نوعي الاستدلال السابقين العكس المستوي conversion و التغيير obversion. مثلا قضية كلية موجبة A ك-م تعارضها سيكون أيضا قضية كلية موجبة A ك-م، وقضية كلية سالبة O ك-س تعارضها سيكون أيضا قضية كلية سالبة O ك-س وهكذا. مثلا “كل المواطنين ناخبين” .. تعارضها هو “كل غير-الناخبين هم غير-مواطنين” .. هذين القضيتين متكافئتين منطقيا. التعارضات صالحة وسليمة منطقيا ويمكن الاستدلال عليها من القضايا الاصلية. لو بدأنا ب “كل س هو ص” .. نعكسها الى “لا يوجد س هو ليس ص” … و تغيرها إلى “لا يوجد ليس ص هو س” الذى من الممكن ان نغيرها الي ” كل ما هو ليس ص ليس س” .. أى أن تعارض اى قضية تأكيد عام هو تغيير انعكاس تغيير القضية الأصلية obverse of the converse of the obverse .. عارف ان عمليات الاستدلال اصبحت معقدة، ودى الفكرة التى حاولت الاشارة لها في بداية الحلقة، من المنظومة البسيطة للقضايا الحملية التي بدأنا بها، صنعنا منظومة كاملة لتحليل القضايا وحقيقة جملها، والاستدلال من قضية الى أخرى باستخدام قواعد منطقية صارمة مثل المعادلات الرياضية، وهذه هي قوة منظومة المنطق الأرسطي التي جعلته لبنة أساسية في علم المنطق للآلاف السنين. على اى حال ان كنت باحث أو دارس لعلم المنطق من المهم ان تكون على دراية بتلك القوانين وقواعد الاستدلال في المنطق الكلاسيكي، لكن بالنسبة للهواة من الكافي ان تدرك ان هناك صور منطقية رياضية للاستدلال على القضايا الحملية بناء على قضايا حملية أخرى، تشكل منظومة قواعد المنطق الكلاسيكي الأرسطي. إذن التعارض أحد صور الاستدلال الصحيح لقضايا الكلية الموجبة ك-م، وهي أيضا صورة صحيحة من الاستدلال المباشر لو طبقناها على قضايا الجزئية السالبة O ج-س . بالرغم من أن القضية الناتجة سيكون تركيبها اللغوى غريب إلا أنها صحيحة منطقيا. مثلا “بعض الطلبة ليسوا مثاليين” .. قضية التعارض المكافئة هي “بعض الغير-مثاليين ليسوا من غير-الطلبة” .. القضية المكافئة للقضية الأولى. لكن التعارض استدلال غير صحيح في حالة الجزئية الموجبة I ج-م .. مثلا “بعض المواطنين هم من غير-السياسيين” .. لو حاولنا الاستدلال على التعارض ستكون الصورة “بعض السياسيين ليسوا من غير-المواطنين” .. ونفس الاستدلال لا يمكن تطبيقة على قضايا الكلية السالبة E ك-س. إذن الصور الاربعة التى يمكن أن يكون عليها الاستدلال بالتعارض Contraposition ..
(1) قضايا الكلية الموجبة A ك-م “كل س هو ص” .. تعارضها ..”كل غير-ص هو غير-س” ..
(2) قضايا الكلية السالبة E ك-س ” لا يوجد س هو ص” الاستدلال بالتعارض غير صحيح
(3) قضايا الجزئية الموجبة I ج-م “بعض س هو ص” .. الاستدلال بالتعارض غير صحيح
(4) وأخيرا قضايا الجزئية السالبة ج-س”بعض س ليس ص” .. الاستدلال بالتعارض هو “بعض غير-ص هو غير-س”. (أنظر الشكل المرافق).
لو تأملت مخططات فين الناتجة ستجد أن قضايا الكلية الموجبة A ك-م متطابقة مع تعارضها ، وقضايا الجزئية السالبة O ج-س أيضا متطابقة مع تعارضها. إذن تعارض الكلية الموجبة والجزئية السالبة لهم نفس قيم الحقيقة اى لهم نفس المعنى، اى متطابقين منطقيا! .. على العكس من قضايا الكلية السالبة E ك-س .. والجزئية الموجبة I ج-م، مخططات فين لقضايا التعارض الناتجة لهم غير مشابهة للمخطط الأصلي، اذن قيمة الحقيقة لتعارض تلك القضايا غير محددة منطقيا، اى لا يمكن الاستدلال على قيمة حقيقية الجملة المتعارضة بمعرفة قيمة الحقيقة للجملة الاصلية. تأمل المثال التالي “(1) لا توجد كلاب هي قطط” (2) اذن، لا توجد غير-قطط هي غير-كلاب” .. المقدمة حقيقة حيث لا توجد كلاب في نفس الوقت قطط. النتيجة لا يمكن التأكد من صحتها منطقيا بمعرفة حقيقة المقدمة لأن المقدمة قضية كلية سالبة E ك-س والنتيجة هي تعارض تلك الجملة التى لا يمكن الاستدلال علي حقيقتها بمعرفة حقيقة المقدمة .. وبالتالي لابد وان نحلل قضية النتيجة بشكل مستقل .. كائن غير-قطة قد يكون الحمار مثلا و كائن غير-كلب قد يكون الحمار أيضا .. إذن لو استبدلنا الفئتين بالحمار .. تصبح جملة النتيجة لا يوجد حمار هو حمار” .. الجملة الغير صحيحة بالقطع “لا يوجد س هو س” .. جملة تخل بأحد قوانين المنطق الثلاثة .. اذن تصبح الحجة ككل غير صالحة.

عادة عند محاولة الاجابة على اسئلة حول العلاقات بين القضايا نلجأ الى الاستدلالات المباشرة التي يمكن أن نطبقها على تلك القضايا كي نحصل على صورة صحيحة أخرى لها تساعدنا على الوصول الى الاجابة. مثلا تأمل تلك القضية “كل الجراحين أطباء” هذة القضية حقيقية. كيف من الممكن أن تساعدنا هذه القضية في التأكد من حقيقة قضية أخرى مثلا “لايوجد غير-جراحين ليسوا غير-أطباء” … بالرغم من غرابة الجملة لغويا إلا أنها قضية من الممكن أن تطرح منطقيا .. الصيغة اللغوية الاسهل لها قد تكون “لايوجد من هم ليسوا جراحين ليسوا من غير الاطباء” … من الممكن ان نستخدم صور الاستدلال المباشر السابقة للتأكد من حقيقة تلك القضية. أولا من الممكن ان نصل الى القضية المعارضة المقابلة “كل غير-الأطباء هم غير-جراحي” .. ثانيا باستخدام التغيير من الممكن أن نشتق “بعض الغير-جراحين هم غير-أطباء” .. لكن هذة القضية مناقضة للقضية محل السؤال وهي “لا يوجد غير-جراحين ليسوا غير-أطباء” .. وبالتالي تصبح الجملة غير صحيحة لأننا اشتقنا قضية صحيحة من القضية الاصلية الصحيحة مناقضة للقضية محل السؤال، إذن تصبح القضية محل السؤال غير صحيحة.
المضمون الوجودي Existential Import
الهدف الأساسي من رحلة بحثنا في القضايا الحملية هو الوصول إلى الدور الذي تلعبة الفرضيات داخل الحجج. قضايا الكلية الموجبة A ك-م وفرضيات الكلية السالبة E ك-س من الممكن تفسيرها بطريقتين مختلفتين. وطبقا لأحد هذين التفسيرين الحجة صالحة وسليمة Valid لكن طبقا للتفسير الآخر الحجة قد تكون خاطئة. لذلك قبل تقييم الحجج لابد وأن نناقش التفسيرين الممكنين للفرضيات الحملية الكلية universal propositions. في بحثنا سنركز على مفهوم المضمون الوجودي existential import. تأمل المثالين الآتيين “كل أفلام أحمد زكي ناجحة” .. “جميع التنانين كائنات مجنحة تبخ النيران” .. في اي محادثة عادية بين فردين حول الفرضية الأولى، يمكن أن نستنتج أن الممثل أحمد  زكي له أفلام. أي أن الجملة لها مضمون وجودي، اى انها تدل أو تفترض ضمنيا وجود شئ ما أو كائنات ما. لكن على الجانب الآخر، الفرضية الثانية قد تكون صحيحة أي أن كل التنانين مجنحة وتبخ النيران، حسب تعريف كائن التنين الأسطوري. لكنه في نهاية الأمر كائن أسطوري، اى ان ليس له وجود في الواقع. وبالتالي يظهر تساؤل مهم، هل يجب تفسير الفرضيات الحملية الكلية على انها تضع فرضيات حول كائنات لها وجود فعلا في الواقع؟ أم أن نطاق تفسيرها يجب أن يمتد لأوسع من هذا أي أن لا يجب أن يكون لها مدلول بالضرورة في عالم الواقع؟ .. في الواقع للتعامل مع هذا التساؤل المنطقيين اتخذوا اتجاهين مختلفين. الأب الروحي للمنطق الكلاسيكي أرسطو Aristotle أعتقد وادعي ان الفرضيات الكلية حول الكائنات والأشياء لابد وان يكون لها مضمون وجودي .. اى انها لابد وان تدل على أشياء أو كائنات لها وجود فعلا في الواقع. مثلا “كل أشجار الصنوبر من القيقب” .. هذة الفرضية تضمن وجود كائن أشجار الصنوبر، لكن “جميع الأشباح كائنات خفية” لا تضمن وجود الاشباح. لان في أفضل صور معرفتنا الموضوعية عن العالم والواقع لا توجد كائنات يطلق عليها الاشباح، على الاقل لا يمكن إثبات هذا من خلال أدلة موضوعية. الرؤية الثانية طورها عالم المنطق الإنجليزي جورج بولي George Boole في القرن التاسع عشر وأكملها من بعده عالم المنطق والرياضيات الإنجليزي جون فين John Venn ومضمونها ببساطة كما توقعت، هو أن لا توجد فرضيات كلية ذات مضمون وجودي. هذه الجمل، الادعاءات، أو الفرضيات لا تدل او تدعي اى شئ عن وجود الاشياء أو الكائنات التي تتحدث عنها. مثلا “كل شاحنات النقل من السيارات” .. لا تدل على وجود شاحنات نقل .. أو “كل المذئوبين وحش دموية” .. أيضا لا تدل على وجود كائنات مذئوبة. إذن من الممكن أن نلخص الرؤية الارسطوطالية في أنها رؤية مفتوحة على الوجود، عندما تتحدث الفرضيات عن أشياء تلك الفرضيات تحمل مضمون وجودي لهذه الأشياء في حالة وجود تلك الأشياء فعلا في الواقع. أي أن الوجود يعد شئ يستدل عليه من خلال الفرضية. على الجانب الآخر الرؤية البولينية Boolean رؤية مغلقة للوجود. اي انها لا تستنتج أو تدل فعلا على وجود الأشياء من الفرضيات الكلية حتى و ان كان هناك وجود فعلا لتلك الأشياء. على النقيض عندما لا توجد الأشياء او الكائنات فعلا في الواقع، لا الرؤية الارسطوطالية ولا الرؤية البولينية تعترف بوجود الكائنات في الواقع، وإلا تصبح الفرضيات غير منطقية، وفي تلك الحالة الرؤية الارسطوطالية تندمج أو تتفق مع الرؤية البولينية!.. الرؤية الارسطوطالية تختلف مع الرؤية البولينية فقط في الفرضيات الكلية الموجبة والسالبة، لكنها تتفق مع الرؤية البولينية في الفرضيات الجزئية الموجبة والسالبة I, O .. كليهما يؤكد أن الفرضيات تقدم دليل او تأكيد على وجود ما. مثلا “بعض القطط من الحيوانات” تؤكد على وجود على الأقل قطة واحدة من الحيوانات، وهذا التفسير مقبول تحت كلا من الرؤية الارسطوطالية والبولينية. وايضا في مثال “بعض الأسماك ليست من الثدييات” .. تؤكد على أن هناك على الأقل سمكة واحدة موجودة ليست من الثدييات. اى ان تحت كلا من التفسير الارسطوطالي والبوليني كلمة “بعض” تتضمن مفهوم وجودي! .. هذا الفرق يؤدى الى فهم الحقيقة المثبتة من خلال الفرضية بصورة مختلفه. اى انك لو اعتنقت الرؤية الارسطوطالية لتفسير الفرضيات التصنيفية العامة، لابد وأن تقبل حقيقة تلك الجمل بمضمونها الوجودي كجزء من دليل الحجة. على العكس لو اعتنقت الرؤية البولينية ستقبل حقيقة الفرضية وتتجاهل المضمون الوجودي لها، اى أنك غير ملزم بالاعتقاد في وجود كائن التنين في الواقع بالرغم من قبول فرضية أن كل التنانين كائنات مجنحة! … ولأن الرؤية البولينية مغلقة تجاه الواقع فهي أبسط من الارسطوطالية التى تفترض تبعات وجودية للكائنات المدعاة في الفرضيات!
زكي له أفلام. أي أن الجملة لها مضمون وجودي، اى انها تدل أو تفترض ضمنيا وجود شئ ما أو كائنات ما. لكن على الجانب الآخر، الفرضية الثانية قد تكون صحيحة أي أن كل التنانين مجنحة وتبخ النيران، حسب تعريف كائن التنين الأسطوري. لكنه في نهاية الأمر كائن أسطوري، اى ان ليس له وجود في الواقع. وبالتالي يظهر تساؤل مهم، هل يجب تفسير الفرضيات الحملية الكلية على انها تضع فرضيات حول كائنات لها وجود فعلا في الواقع؟ أم أن نطاق تفسيرها يجب أن يمتد لأوسع من هذا أي أن لا يجب أن يكون لها مدلول بالضرورة في عالم الواقع؟ .. في الواقع للتعامل مع هذا التساؤل المنطقيين اتخذوا اتجاهين مختلفين. الأب الروحي للمنطق الكلاسيكي أرسطو Aristotle أعتقد وادعي ان الفرضيات الكلية حول الكائنات والأشياء لابد وان يكون لها مضمون وجودي .. اى انها لابد وان تدل على أشياء أو كائنات لها وجود فعلا في الواقع. مثلا “كل أشجار الصنوبر من القيقب” .. هذة الفرضية تضمن وجود كائن أشجار الصنوبر، لكن “جميع الأشباح كائنات خفية” لا تضمن وجود الاشباح. لان في أفضل صور معرفتنا الموضوعية عن العالم والواقع لا توجد كائنات يطلق عليها الاشباح، على الاقل لا يمكن إثبات هذا من خلال أدلة موضوعية. الرؤية الثانية طورها عالم المنطق الإنجليزي جورج بولي George Boole في القرن التاسع عشر وأكملها من بعده عالم المنطق والرياضيات الإنجليزي جون فين John Venn ومضمونها ببساطة كما توقعت، هو أن لا توجد فرضيات كلية ذات مضمون وجودي. هذه الجمل، الادعاءات، أو الفرضيات لا تدل او تدعي اى شئ عن وجود الاشياء أو الكائنات التي تتحدث عنها. مثلا “كل شاحنات النقل من السيارات” .. لا تدل على وجود شاحنات نقل .. أو “كل المذئوبين وحش دموية” .. أيضا لا تدل على وجود كائنات مذئوبة. إذن من الممكن أن نلخص الرؤية الارسطوطالية في أنها رؤية مفتوحة على الوجود، عندما تتحدث الفرضيات عن أشياء تلك الفرضيات تحمل مضمون وجودي لهذه الأشياء في حالة وجود تلك الأشياء فعلا في الواقع. أي أن الوجود يعد شئ يستدل عليه من خلال الفرضية. على الجانب الآخر الرؤية البولينية Boolean رؤية مغلقة للوجود. اي انها لا تستنتج أو تدل فعلا على وجود الأشياء من الفرضيات الكلية حتى و ان كان هناك وجود فعلا لتلك الأشياء. على النقيض عندما لا توجد الأشياء او الكائنات فعلا في الواقع، لا الرؤية الارسطوطالية ولا الرؤية البولينية تعترف بوجود الكائنات في الواقع، وإلا تصبح الفرضيات غير منطقية، وفي تلك الحالة الرؤية الارسطوطالية تندمج أو تتفق مع الرؤية البولينية!.. الرؤية الارسطوطالية تختلف مع الرؤية البولينية فقط في الفرضيات الكلية الموجبة والسالبة، لكنها تتفق مع الرؤية البولينية في الفرضيات الجزئية الموجبة والسالبة I, O .. كليهما يؤكد أن الفرضيات تقدم دليل او تأكيد على وجود ما. مثلا “بعض القطط من الحيوانات” تؤكد على وجود على الأقل قطة واحدة من الحيوانات، وهذا التفسير مقبول تحت كلا من الرؤية الارسطوطالية والبولينية. وايضا في مثال “بعض الأسماك ليست من الثدييات” .. تؤكد على أن هناك على الأقل سمكة واحدة موجودة ليست من الثدييات. اى ان تحت كلا من التفسير الارسطوطالي والبوليني كلمة “بعض” تتضمن مفهوم وجودي! .. هذا الفرق يؤدى الى فهم الحقيقة المثبتة من خلال الفرضية بصورة مختلفه. اى انك لو اعتنقت الرؤية الارسطوطالية لتفسير الفرضيات التصنيفية العامة، لابد وأن تقبل حقيقة تلك الجمل بمضمونها الوجودي كجزء من دليل الحجة. على العكس لو اعتنقت الرؤية البولينية ستقبل حقيقة الفرضية وتتجاهل المضمون الوجودي لها، اى أنك غير ملزم بالاعتقاد في وجود كائن التنين في الواقع بالرغم من قبول فرضية أن كل التنانين كائنات مجنحة! … ولأن الرؤية البولينية مغلقة تجاه الواقع فهي أبسط من الارسطوطالية التى تفترض تبعات وجودية للكائنات المدعاة في الفرضيات!

مربع التقابل الحديث Modern Square of Opposition
العلاقة بين أزواج القضايا المتقابلة بشكل تبادلي التى ناقشناها منذ قليل، ومثلناها في المخطط المهم جدا في المنطق الكلاسيكي المعروف بمربع التقابل الحديث modern square of opposition (أنظر الشكل المرافق) .. هذا المخطط قائم على الصورة الكلاسيكية منة المعروفة بمربع أرسطو، لكنه يعتنق المنطق البوليني وتفسيره للقضايا الحملية من حيث المفهوم الوجودي. أهمية هذا المخطط انه يساعدنا على الاستدلال على حقيقة قضية حملية من خلال قضية أخرى. لو القضيتين بينهما علاقة تناقض contradictory relation كما في حالة قضايا الكلية الموجبة ك-م A وقضايا الجزئية السالبة ج-س O أو في حالة قضايا الكلية السالبة ك-س E وقضايا الجزئية الموجبة ج-م I. إذن لو هناك قضية كلية عامة صحيحة لابد وأن قضية الجزئية السالبة المقابلة لها لابد وأن تكون خاطئة! وبنفس الصورة قضية كلية سالبة صحيحة لابد وأن قضية الجزئية الموجبة المقابلة لها تكون خاطئة. لكننا لانستطيع ان نستدل على حقيقة قضية الكلية السالبة المقابلة لقضية الكلية الموجبة مثلا لان قيمة الحقيقة غير محددة منطقيا من خلال العلاقات بين تلك القضايا في مربع التقابل logically undetermined truth value اى ببساطة هذين القضيتين غير متقابلتين. إذن لا يمكن الاستدلال على حقيقة واحدة منهم بمعرفة حقيقة الاخرى. ونفس الفكرة يمكن تطبيقها على العلاقة بين قضايا الكلية السالبة ك-س E وقضايا الجزئية السالبة ج-س O، وهكذا انظر مخطط مربع التقابل للتعرف على باقي العلاقات الغير محددة منطقيا. والآن سأطرح عليك فكرة غالبا ستكون واحدة من أغرب الأفكار التى سمعتها من قبل، تخيل أن أمامنا أربع قضايا حملية حول كائن ليس له وجود في الواقع مثلا كائن الحصان المجنح. في حالة قضية كلية موجبة A ك-م تحاول إثبات أن كل الاحصنة المجنحة تنتمي لفئة أسناد اخرى، ستكون قضية صحيحة لان لا يوجد اى احصنة مجنحة في الواقع وبالتالي فعلا كل الاحصنة المجنحة (التي هي صفر في تلك الحالة) تنتمي لفئة الاسناد! … الأمر الصحيح لأن صفر ينتمي لكل الفئات. ونفس الفكرة تنطبق على قضية الكلية السالبة ك-س E أيضا ستكون صحيحة لان لا يوجد اى احصنة مجنحة وبالتالي من الصحيح الادعاء ان لايوجد اى احصنة مجنحة جزء من فئة الاسناد. هذة القضايا يطلق عليها في المنطق الكلاسيكي “صحيحة بشكل خاطئ vacuously true ” .. نعم صحيحة بشكل خاطئ .. مصطلح غريب لو بتسمعة للمرة الأولى، هذا لأن قيمة الحقيقة للقضايا نتجت فقط بسبب أن فئة الموضوع (الاحصنة المجنحة) ليس لها وجود اى انها فئة فارغة لا يوجد بها عناصر. ده بالاضافة لان قيمة الحقيقة لتلك القضايا لا تتعارض مع العلاقات الغير محددة منطقية في مربع التقابل بين القضية A و E .. ليس بسبب العلاقة بينهم لكن ببساطة لأن فئة الموضوع فارغة. وبنفس الفكرة، خطأ حقيقة القضايا الجزئية في حالة الإيجاب I والسلب O يقال انها خاطئة بشكل باطل vacuously false. إذن أهمية مخطط مربع التقابل أنه يقدم نتائج ضرورية منطقيا، اى ان لايوجد مفر من صحتها. وبالتالي من الممكن أن نستخدمها للتأكد من صلاحية الحجج. نبدأ بافتراض أن مقدمة الحجة حقيقية، ونضع قيمة حقيقة المقدمة داخل مخطط التعارض باستخدام المخطط نستدل على قيمة الحقيقة لباقي الفرضيات المقابلة، ومن خلال تلك الحقائق نستنتج قيمة الحقيقة لنتيجة الحجة لو ظهر أن نتيجة الحجة حقيقية إذن الحجة صالحة وسليمة. مثلا “بعض الجواسيس غير محترفين في القتل .. لذا من الخطأ أن كل الجواسيس محترفين في القتل” .. حجة من هذا النوع يطلق عليها حجة استدلال مباشر immediate inferences لان بها مقدمة واحدة فقط، بدلا من الانتقال من مقدمة أولى الى مقدمة وسيطة ثم الى النتيجة، نستدل مباشرة على حقيقة النتيجة من المقدمة. كي نختبر صلاحية تلك الحجة، سنبدأ بافتراض أن المقدمة حقيقية، المقدمة هي قضية جزئية سالبة ج-س O ، ثم نضع قيمة الحقيقة لها في مربع التقابل ، ومنه نستدل على قيمة الحقيقة للقضية التصنيفية المقابلة في تلك الحالة هي قضية الكلية الموجبة ك-م A، المقابلة لها من خلال علاقة التناقض، قضية الكلية الموجبة لابد وأن تكون خاطئة في حالة صحة الجزئية السالبة. نتيجة الحجة تقر بأن من الخطأ أن كل الجواسيس محترفين في القتل، اى أنها تقر بأن التأكيد الكلي خاطئ. إذن النتيجة صحيحة، وبالتالي الحجة صالحة Valid. الحجج الصالحة من وجهة النظر البولينية يقال إنها غير مشروطة الصلاحية unconditionally valid لأنها صالحة سواء كانت المصطلحات المستخدمة فيها تشير الى كائنات لها وجود في الواقع أم لا. مثال آخر … ” من الخطأ أن كل الحيوانات كلاب، اذن، لايوجد حيوانات من الكلاب” … سنبدأ بـ افتراض ان المقدمة حقيقية، بما ان المقدمة تدعي ان قضية كلية موجبة ك-م A خاطئة لأنها تقر بأن من الخطأ ان كل الحيوانات كلاب، سنضع في مربع التقابل خطأ في مكان قضية ك-م A .. ثم نحاول الاستدلال على قيمة قضية الكلية السالبة ك-س E، لانها هي القضية التصنيفية في النتيجة “لا يوجد حيوانات من الكلاب” .. لكن لو تأملت المخطط لا توجد علاقة تربط الكلية الموجبة، و الكلية السالبة، إذن قيمة الحقيقة للكلية السلبية ك-س E غير محددة. إذن قيمة الحقيقة لنتيجة الحجة غير محددة وبالتالي تصبح الحجة غير صالحة Invalid. مثال آخر “كل التليفونات الذكية أجهزة لاسلكية .. لذا، بعض التليفونات الذكية، أجهزة لاسلكية” … من الممكن أن تستدل على صلاحية تلك الحجة باستخدام مخططات فين، المقدمة ستكون على صورة دائرتين متقاطعتين فيها المنطقة اليسرى من دائرة التليفونات الذكية مخططة اى انها فارغة، اى لايوجد اى اى تليفونات ذكية ليست لاسلكية، ومخطط النتيجة، سيكون على صورة دائرتين متقاطعتين، والمنطقة اليمنى من دائرة التليفونات الذكية (منطقة التقاطع) بها علامة X .. أى أن هناك على الأقل عنصر واحد في تلك المنطقة، أي أن بعض التليفونات الذكية لاسلكية (أنظر الشكل المرافق) ، هذين المخططين على النقيض من بعضهما البعض، اى لايمكن أن يكونا صحيحين في نفس الوقت، إذن الاستدلال من المقدمة على النتيجة غير صحيح، أى أن الحجة غير صالحة، ويمكنك أيضا التأكد من صحة هذه النتيجة باستخدام مخطط ساحة التعارض. الحجج من هذا النوع يقال انها ارتكبت المغالطة الوجودية existential fallacy.
.. هذا المخطط قائم على الصورة الكلاسيكية منة المعروفة بمربع أرسطو، لكنه يعتنق المنطق البوليني وتفسيره للقضايا الحملية من حيث المفهوم الوجودي. أهمية هذا المخطط انه يساعدنا على الاستدلال على حقيقة قضية حملية من خلال قضية أخرى. لو القضيتين بينهما علاقة تناقض contradictory relation كما في حالة قضايا الكلية الموجبة ك-م A وقضايا الجزئية السالبة ج-س O أو في حالة قضايا الكلية السالبة ك-س E وقضايا الجزئية الموجبة ج-م I. إذن لو هناك قضية كلية عامة صحيحة لابد وأن قضية الجزئية السالبة المقابلة لها لابد وأن تكون خاطئة! وبنفس الصورة قضية كلية سالبة صحيحة لابد وأن قضية الجزئية الموجبة المقابلة لها تكون خاطئة. لكننا لانستطيع ان نستدل على حقيقة قضية الكلية السالبة المقابلة لقضية الكلية الموجبة مثلا لان قيمة الحقيقة غير محددة منطقيا من خلال العلاقات بين تلك القضايا في مربع التقابل logically undetermined truth value اى ببساطة هذين القضيتين غير متقابلتين. إذن لا يمكن الاستدلال على حقيقة واحدة منهم بمعرفة حقيقة الاخرى. ونفس الفكرة يمكن تطبيقها على العلاقة بين قضايا الكلية السالبة ك-س E وقضايا الجزئية السالبة ج-س O، وهكذا انظر مخطط مربع التقابل للتعرف على باقي العلاقات الغير محددة منطقيا. والآن سأطرح عليك فكرة غالبا ستكون واحدة من أغرب الأفكار التى سمعتها من قبل، تخيل أن أمامنا أربع قضايا حملية حول كائن ليس له وجود في الواقع مثلا كائن الحصان المجنح. في حالة قضية كلية موجبة A ك-م تحاول إثبات أن كل الاحصنة المجنحة تنتمي لفئة أسناد اخرى، ستكون قضية صحيحة لان لا يوجد اى احصنة مجنحة في الواقع وبالتالي فعلا كل الاحصنة المجنحة (التي هي صفر في تلك الحالة) تنتمي لفئة الاسناد! … الأمر الصحيح لأن صفر ينتمي لكل الفئات. ونفس الفكرة تنطبق على قضية الكلية السالبة ك-س E أيضا ستكون صحيحة لان لا يوجد اى احصنة مجنحة وبالتالي من الصحيح الادعاء ان لايوجد اى احصنة مجنحة جزء من فئة الاسناد. هذة القضايا يطلق عليها في المنطق الكلاسيكي “صحيحة بشكل خاطئ vacuously true ” .. نعم صحيحة بشكل خاطئ .. مصطلح غريب لو بتسمعة للمرة الأولى، هذا لأن قيمة الحقيقة للقضايا نتجت فقط بسبب أن فئة الموضوع (الاحصنة المجنحة) ليس لها وجود اى انها فئة فارغة لا يوجد بها عناصر. ده بالاضافة لان قيمة الحقيقة لتلك القضايا لا تتعارض مع العلاقات الغير محددة منطقية في مربع التقابل بين القضية A و E .. ليس بسبب العلاقة بينهم لكن ببساطة لأن فئة الموضوع فارغة. وبنفس الفكرة، خطأ حقيقة القضايا الجزئية في حالة الإيجاب I والسلب O يقال انها خاطئة بشكل باطل vacuously false. إذن أهمية مخطط مربع التقابل أنه يقدم نتائج ضرورية منطقيا، اى ان لايوجد مفر من صحتها. وبالتالي من الممكن أن نستخدمها للتأكد من صلاحية الحجج. نبدأ بافتراض أن مقدمة الحجة حقيقية، ونضع قيمة حقيقة المقدمة داخل مخطط التعارض باستخدام المخطط نستدل على قيمة الحقيقة لباقي الفرضيات المقابلة، ومن خلال تلك الحقائق نستنتج قيمة الحقيقة لنتيجة الحجة لو ظهر أن نتيجة الحجة حقيقية إذن الحجة صالحة وسليمة. مثلا “بعض الجواسيس غير محترفين في القتل .. لذا من الخطأ أن كل الجواسيس محترفين في القتل” .. حجة من هذا النوع يطلق عليها حجة استدلال مباشر immediate inferences لان بها مقدمة واحدة فقط، بدلا من الانتقال من مقدمة أولى الى مقدمة وسيطة ثم الى النتيجة، نستدل مباشرة على حقيقة النتيجة من المقدمة. كي نختبر صلاحية تلك الحجة، سنبدأ بافتراض أن المقدمة حقيقية، المقدمة هي قضية جزئية سالبة ج-س O ، ثم نضع قيمة الحقيقة لها في مربع التقابل ، ومنه نستدل على قيمة الحقيقة للقضية التصنيفية المقابلة في تلك الحالة هي قضية الكلية الموجبة ك-م A، المقابلة لها من خلال علاقة التناقض، قضية الكلية الموجبة لابد وأن تكون خاطئة في حالة صحة الجزئية السالبة. نتيجة الحجة تقر بأن من الخطأ أن كل الجواسيس محترفين في القتل، اى أنها تقر بأن التأكيد الكلي خاطئ. إذن النتيجة صحيحة، وبالتالي الحجة صالحة Valid. الحجج الصالحة من وجهة النظر البولينية يقال إنها غير مشروطة الصلاحية unconditionally valid لأنها صالحة سواء كانت المصطلحات المستخدمة فيها تشير الى كائنات لها وجود في الواقع أم لا. مثال آخر … ” من الخطأ أن كل الحيوانات كلاب، اذن، لايوجد حيوانات من الكلاب” … سنبدأ بـ افتراض ان المقدمة حقيقية، بما ان المقدمة تدعي ان قضية كلية موجبة ك-م A خاطئة لأنها تقر بأن من الخطأ ان كل الحيوانات كلاب، سنضع في مربع التقابل خطأ في مكان قضية ك-م A .. ثم نحاول الاستدلال على قيمة قضية الكلية السالبة ك-س E، لانها هي القضية التصنيفية في النتيجة “لا يوجد حيوانات من الكلاب” .. لكن لو تأملت المخطط لا توجد علاقة تربط الكلية الموجبة، و الكلية السالبة، إذن قيمة الحقيقة للكلية السلبية ك-س E غير محددة. إذن قيمة الحقيقة لنتيجة الحجة غير محددة وبالتالي تصبح الحجة غير صالحة Invalid. مثال آخر “كل التليفونات الذكية أجهزة لاسلكية .. لذا، بعض التليفونات الذكية، أجهزة لاسلكية” … من الممكن أن تستدل على صلاحية تلك الحجة باستخدام مخططات فين، المقدمة ستكون على صورة دائرتين متقاطعتين فيها المنطقة اليسرى من دائرة التليفونات الذكية مخططة اى انها فارغة، اى لايوجد اى اى تليفونات ذكية ليست لاسلكية، ومخطط النتيجة، سيكون على صورة دائرتين متقاطعتين، والمنطقة اليمنى من دائرة التليفونات الذكية (منطقة التقاطع) بها علامة X .. أى أن هناك على الأقل عنصر واحد في تلك المنطقة، أي أن بعض التليفونات الذكية لاسلكية (أنظر الشكل المرافق) ، هذين المخططين على النقيض من بعضهما البعض، اى لايمكن أن يكونا صحيحين في نفس الوقت، إذن الاستدلال من المقدمة على النتيجة غير صحيح، أى أن الحجة غير صالحة، ويمكنك أيضا التأكد من صحة هذه النتيجة باستخدام مخطط ساحة التعارض. الحجج من هذا النوع يقال انها ارتكبت المغالطة الوجودية existential fallacy.

المغالطة الوجودية Existential Fallacy
المغالطة الوجودية تحدث عندما تكون الحجة خاطئة لان المقدمة تفتقد للمضمون الوجودي existential import الحجج من هذا النوع عادة ما تكون مقدمتها قضايا كلية ونتائجها قضايا جزئية، المغالطة تحدث لاننا نحاول ان نستدل على نتيجة ذات مضمون وجودي أي لها تبعات وجودية فيما يوجد في الواقع من مقدمة تفتقد لهذا المضمون. في الحقيقة التعرف على المغالطات الوجودية سهل جدا لو أستخدمت مخططات فين، لو ظهر في المخطط جزء من الدائرة مظلل في المقدمة لكن الجزء المعاكس لة من نفس الدائرة بة علامة X في مخطط النتيجة، إذن الحجة ارتكبت المغالطة الوجودية، هذة مثلا بعض الصور التى من الممكن أن تحدث بها المغالطة “كل س هو ص .. إذن، بعض س هو ص” ، “من الخطأ أن بعض س هو ص .. إذن من الخطأ ان لا يوجد س هو ص” … “لايوجد س هو ص .. إذن، من الخطأ أن كل س هو ص” .. “من الخطأ أن بعض س هو ص … إذن، بعض س هو ص” ..الخ. لو لاحظت في كل تلك الامثلة، الحجة تنتقل من قضية كلية لا تحتوى على مضمون وجودي اى لاتثبت اى شئ عن حقيقة وجود الكائنات في الواقع (طبقا للتفسير البوليني) إلى قضية جزئية في النتيجة لها مضمون وجودي (اى تثبت وجود الكائن في الواقع طبقا للتفسير البوليني) .. لكن من المهم أن تلاحظ ان ليست كل حجة تحتوى على قضية كلية وقضية جزئية ترتكب المغالطة الوجودية .. مثلا “كل س هو ص .. إذن بعض س ليس ص” .. هذة الحجة غير صالحة لأن النتيجة تناقض المقدمة، لكنها لم ترتكب المغالطة الوجودية، اذن كي نعرف إن كانت الحجة ارتكبت المغالطة لابد من التأكد أن سبب عدم صلاحية الحجة نشأ عن فقدان المضمون الوجودي في المقدمة والاستدلال عليه في النتيجة، الأمر الذي يمكن التعرف عليه بسهولة من خلال مخططات فين.

جوهر منطق أرسطو Aristotle Logic Foundation
جوهر المنطق الكلاسيكي أو منطق أرسطو هو أنواع القضايا الأربعة التى بنى عليها أرسطو منظومته المنطقية، القضايا الكلية الموجبة ك-م A، القضايا الكلية السالبة ك-س E، القضايا الجزئية الموجبة ج-م I، القضايا الجزئية السالبة ج-س O. هذة القضايا الاربعة هى التى بنى عليها كل القواعد المنطقية التى تعرضنا لها منذ قليل. لو لاحظت في تلك القضايا معامل الكيف والكم دائما نفس النوع لفئة الموضوع. لكن الجمل والقضايا قد تحتوى على مزيج من المعاملات المختلفة لكن أرسطو تجنبها عند بنائه منظومته المنطقية عند قصد. مثلا جملة على صيغة “كل النقاد أثنوا على بعض أفلام أحمد زكى” أو جملة “بعض النقاد أثنوا على كل أفلام أحمد زكي” .. جمل امتزج فيها صورتي معامل الكم، الكلي  والجزئي. وهناك صور أكثر تعقيدا خصوصا ان أمتزج فيها صورتي معامل الكيف أيضا الإيجاب والسلب. تأمل هذه القضايا “لم يستمتع كل النقاد بكل أفلام أحمد زكي” .. أو “بعض النقاد لم يستمتعوا بكل أفلام أحمد زكي” .. أو “بعض النقاد لم يستمتعوا ببعض أفلام أحمد زكي” .. واخيرا “كل النقاد لم يستمتعوا بكل أفلام أحمد زكي” .. بتوزيع معامل الكم والكيف على فئة الموضوع وفئة المحمول نحصل على صور جديدة من القضايا الحملية، بعضها أكثر تعقيدا من الاخر، وبعضها يأكد نفس الفكرة لكن بصورة مختلفة. سنة 1846 الفيلسوف والمنطقي الاسكتلندي وليام هاميلتون من ادنبره Sir William Hamilton of Edinburgh في مقال بعنوان “تحليل جديد للشكل المنطقي New Analytic of Logical Form” طرح ثمان صور للقضايا الحملية. هذه الصور كالآتي
والجزئي. وهناك صور أكثر تعقيدا خصوصا ان أمتزج فيها صورتي معامل الكيف أيضا الإيجاب والسلب. تأمل هذه القضايا “لم يستمتع كل النقاد بكل أفلام أحمد زكي” .. أو “بعض النقاد لم يستمتعوا بكل أفلام أحمد زكي” .. أو “بعض النقاد لم يستمتعوا ببعض أفلام أحمد زكي” .. واخيرا “كل النقاد لم يستمتعوا بكل أفلام أحمد زكي” .. بتوزيع معامل الكم والكيف على فئة الموضوع وفئة المحمول نحصل على صور جديدة من القضايا الحملية، بعضها أكثر تعقيدا من الاخر، وبعضها يأكد نفس الفكرة لكن بصورة مختلفة. سنة 1846 الفيلسوف والمنطقي الاسكتلندي وليام هاميلتون من ادنبره Sir William Hamilton of Edinburgh في مقال بعنوان “تحليل جديد للشكل المنطقي New Analytic of Logical Form” طرح ثمان صور للقضايا الحملية. هذه الصور كالآتي
(1) كل س هو كل ص
(2) كل س هو بعض ص
(3) بعض س هو كل ص
(4) بعض س هو بعض ص
(5) أي س هو ليس اي من ص
(6)أي س ليس بعض ص
(7) بعض س ليس أي من ص
(8) بعض س هو ليس أيا من ص.
بالرغم ان للوهلة الأولى هذة المنظومة تبدو أكثر اكتمالا من منظومة أرسطو لأنها تغطي عدد اكبر من القضايا الحملية وتستخدم توزيعات أكثر لكلا من معامل الكم والكيف. الا ان هناك العديد من المشاكل المتعلقة بمنظومة هاميلتون المنطقية. وهذة الورقة البحثية قادت إلى الخلاف الشهير بينه وبين الرياضي الإنجليزي أغسطس دي مورجان Augustus De Morgan . أحد نقاط هذا الخلاف كان حول تعريف هاميلتون لمصطلح “بعض”. الذي رأى ان بعض تعني فقط بعض وليس واحد علي الاقل كما أعتقد أرسطو. لكن هل “بعض” يعني “بعض على الاكثر” أم “بعض على الاقل”، أم “البعض وليس البقية”؟ … دي مورجان أصر على ان تعريف هاميلتون ل “بعض” ملتبس وغامض. وجادل في كتابه “عن  القياس On the Syllogism” كالاتي “هنا بعض .. كمية غامضة تمامًا في اتجاه واحد: إنها ليست لا شيء ؛ و لا واحد على الأقل ؛ أو أكثر ؛ أو الكل. بعض ، في الاستخدام اليومي ، غالبًا ما تعني كلا من ليس لا شيء وأيضا ليس كل شيء ؛ لكن في المنطق، تعني فقط ليس لا شيء؟” .. الفيلسوف والمنطقي الأمريكي تشارلز ساندرز بيرس Charles Sanders Peirce أتفق مع دي مورجان وجادل في أن “بعض” يجب أن تعني “أكثر من لاشئ”. وفي الحقيقة محاولة هاميلتون لتطوير المنطق الارسطي لم يحالفها الحظ، وفشلت تماما. تفاصيل منظومة هاميلتون المنطقية والخلاف الذي دار حولها تبقي قصة قاصرة على المتخصصين والباحثين لكن أهميتها تكمن في سر قوة منظومة منطق أرسطو الكلاسيكية، وهو البساطة، التى مكنتها تقريبا ان تبقى دون أى تعديلات جوهرية لأكثر من الفين عام. فقط باستخدام أربع أنواع من القضايا أرسطو بنى منظومة كاملة للحجج المنطقية من الممكن أن نعتمد عليها كي نصل الى حقيقة الحجة. والتي أصبحت تعرف فيما بعد بمنطق القياس syllogisms الذي دائما ما يقود الى نتيجة سليمة لكن ايضا يستخدم لكشف الحجج الغير صالحة.
القياس On the Syllogism” كالاتي “هنا بعض .. كمية غامضة تمامًا في اتجاه واحد: إنها ليست لا شيء ؛ و لا واحد على الأقل ؛ أو أكثر ؛ أو الكل. بعض ، في الاستخدام اليومي ، غالبًا ما تعني كلا من ليس لا شيء وأيضا ليس كل شيء ؛ لكن في المنطق، تعني فقط ليس لا شيء؟” .. الفيلسوف والمنطقي الأمريكي تشارلز ساندرز بيرس Charles Sanders Peirce أتفق مع دي مورجان وجادل في أن “بعض” يجب أن تعني “أكثر من لاشئ”. وفي الحقيقة محاولة هاميلتون لتطوير المنطق الارسطي لم يحالفها الحظ، وفشلت تماما. تفاصيل منظومة هاميلتون المنطقية والخلاف الذي دار حولها تبقي قصة قاصرة على المتخصصين والباحثين لكن أهميتها تكمن في سر قوة منظومة منطق أرسطو الكلاسيكية، وهو البساطة، التى مكنتها تقريبا ان تبقى دون أى تعديلات جوهرية لأكثر من الفين عام. فقط باستخدام أربع أنواع من القضايا أرسطو بنى منظومة كاملة للحجج المنطقية من الممكن أن نعتمد عليها كي نصل الى حقيقة الحجة. والتي أصبحت تعرف فيما بعد بمنطق القياس syllogisms الذي دائما ما يقود الى نتيجة سليمة لكن ايضا يستخدم لكشف الحجج الغير صالحة.
ودلوقتي .. تأمل الصور الاربعة لقضايا المنطق الكلاسيكي .. ما هو يا ترى سر قوة وبقاء المنظومة لآلاف السنين؟ … هل هي البساطة ؟ .. أم الاتساق؟ … وإن كانت الحجة سليمة هل يعني هذا أن لها مضمون وجودي؟ .. وإن لم يكن للحجج مضمون وجودي، ما هي طبيعة الحقيقة الناتجة عن الحجة؟ … فكر تاني
في الحلقة الجاية .. سنعود في الزمن لأكثر من ألفين عام، كي نكمل رحلة بحثنا في أعماق المنطق الكلاسيكي .. عن أشكال القياس القياسية … طبيعة الحجج القياسية … قواعد القياس … والاستدلال التراكمي .. هنتفلسف المرة الجاية.
من دلوقتي للحلقة الجاية .. عيش الحياة بفلسفة!
الحلقة بدون خلفية موسيقية
زود معلوماتك:
- Hurley, P. J. – A Concise Introduction to Logic, 13th ed (2018)
- Hausman, Alan; Kahane, Howard; Tidman, Paul. – Logic and Philosophy: A Modern Introduction. 12th edition (2013)
- Copi, Irving and Cohen, Carl. – Introduction to Logic. 14th ed (2010)
- Grayling, A. C. – An Introduction to Philosophical Logic (2001)
- Girle, Rod. – Modal Logics and Philosophy (2000)
- Wittgenstein, Ludwig – Philosophical Investigations (1958)
- Frege, Gottlob – The Foundations of Arithmetic (1884)
- Ayer, A. J. – Language, Truth and Logic (1946
القضايا الحملية Categorical Propositions
المنطق الأرسطي Aristotelian Logic
أرسطو Aristotle
الاورغانون Organon
مخططات فيين Venn diagrams
جورج بولي George Boole
مربع ارسطو The Traditional Square of Opposition
العكس المستوى Conversion
الاستدلال بنقض المحمول (التغيير) Obversion
الاستدلال بالتعارض Contraposition
المضمون الوجودي Existential Import
المغالطة الوجودية Existential Fallacy
وليام هاميلتون من ادنبره Sir William Hamilton of Edinburgh
أغسطس دي مورجان Augustus De Morgan
Music Credit
===========
Naseer Shamma – Happened at All: Amiriyaa
myuu – Fernweh
Celtic Music – Child of the Highlands
Dark Piano – Liar
myuu – Look Out
myuu – Angst
myuu – Suspicious
myuu – Spook Box
myuu – Bittersweet
myuu – Carmen Habanera
Kevin MacLeod – Pooka
للتواصل ومتابعة باقى الحلقات تابعونا على:
https://www.facebook.com/KalamFalsfa
https://kalamfalsfa.wordpress.com
https://plus.google.com/u/0/+KalamFalsfa